Assignment Problem: Meaning, Methods and Variations | Operations Research
After reading this article you will learn about:- 1. Meaning of Assignment Problem 2. Definition of Assignment Problem 3. Mathematical Formulation 4. Hungarian Method 5. Variations.

Meaning of Assignment Problem:
An assignment problem is a particular case of transportation problem where the objective is to assign a number of resources to an equal number of activities so as to minimise total cost or maximize total profit of allocation.
The problem of assignment arises because available resources such as men, machines etc. have varying degrees of efficiency for performing different activities, therefore, cost, profit or loss of performing the different activities is different.
Thus, the problem is “How should the assignments be made so as to optimize the given objective”. Some of the problem where the assignment technique may be useful are assignment of workers to machines, salesman to different sales areas.
Definition of Assignment Problem:
ADVERTISEMENTS:
Suppose there are n jobs to be performed and n persons are available for doing these jobs. Assume that each person can do each job at a term, though with varying degree of efficiency, let c ij be the cost if the i-th person is assigned to the j-th job. The problem is to find an assignment (which job should be assigned to which person one on-one basis) So that the total cost of performing all jobs is minimum, problem of this kind are known as assignment problem.
The assignment problem can be stated in the form of n x n cost matrix C real members as given in the following table:
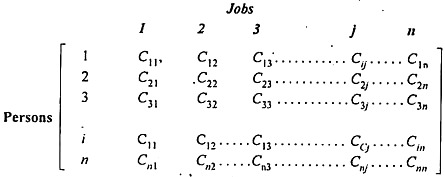
The Hungarian method is a computational optimization technique that addresses the assignment problem in polynomial time and foreshadows following primal-dual alternatives. In 1955, Harold Kuhn used the term “Hungarian method” to honour two Hungarian mathematicians, Dénes Kőnig and Jenő Egerváry. Let’s go through the steps of the Hungarian method with the help of a solved example.
Hungarian Method to Solve Assignment Problems
The Hungarian method is a simple way to solve assignment problems. Let us first discuss the assignment problems before moving on to learning the Hungarian method.
What is an Assignment Problem?
A transportation problem is a type of assignment problem. The goal is to allocate an equal amount of resources to the same number of activities. As a result, the overall cost of allocation is minimised or the total profit is maximised.
Because available resources such as workers, machines, and other resources have varying degrees of efficiency for executing different activities, and hence the cost, profit, or loss of conducting such activities varies.
Assume we have ‘n’ jobs to do on ‘m’ machines (i.e., one job to one machine). Our goal is to assign jobs to machines for the least amount of money possible (or maximum profit). Based on the notion that each machine can accomplish each task, but at variable levels of efficiency.
Hungarian Method Steps
Check to see if the number of rows and columns are equal; if they are, the assignment problem is considered to be balanced. Then go to step 1. If it is not balanced, it should be balanced before the algorithm is applied.
Step 1 – In the given cost matrix, subtract the least cost element of each row from all the entries in that row. Make sure that each row has at least one zero.
Step 2 – In the resultant cost matrix produced in step 1, subtract the least cost element in each column from all the components in that column, ensuring that each column contains at least one zero.
Step 3 – Assign zeros
- Analyse the rows one by one until you find a row with precisely one unmarked zero. Encircle this lonely unmarked zero and assign it a task. All other zeros in the column of this circular zero should be crossed out because they will not be used in any future assignments. Continue in this manner until you’ve gone through all of the rows.
- Examine the columns one by one until you find one with precisely one unmarked zero. Encircle this single unmarked zero and cross any other zero in its row to make an assignment to it. Continue until you’ve gone through all of the columns.
Step 4 – Perform the Optimal Test
- The present assignment is optimal if each row and column has exactly one encircled zero.
- The present assignment is not optimal if at least one row or column is missing an assignment (i.e., if at least one row or column is missing one encircled zero). Continue to step 5. Subtract the least cost element from all the entries in each column of the final cost matrix created in step 1 and ensure that each column has at least one zero.
Step 5 – Draw the least number of straight lines to cover all of the zeros as follows:
(a) Highlight the rows that aren’t assigned.
(b) Label the columns with zeros in marked rows (if they haven’t already been marked).
(c) Highlight the rows that have assignments in indicated columns (if they haven’t previously been marked).
(d) Continue with (b) and (c) until no further marking is needed.
(f) Simply draw the lines through all rows and columns that are not marked. If the number of these lines equals the order of the matrix, then the solution is optimal; otherwise, it is not.
Step 6 – Find the lowest cost factor that is not covered by the straight lines. Subtract this least-cost component from all the uncovered elements and add it to all the elements that are at the intersection of these straight lines, but leave the rest of the elements alone.
Step 7 – Continue with steps 1 – 6 until you’ve found the highest suitable assignment.
Hungarian Method Example
Use the Hungarian method to solve the given assignment problem stated in the table. The entries in the matrix represent each man’s processing time in hours.
\(\begin{array}{l}\begin{bmatrix} & I & II & III & IV & V \\1 & 20 & 15 & 18 & 20 & 25 \\2 & 18 & 20 & 12 & 14 & 15 \\3 & 21 & 23 & 25 & 27 & 25 \\4 & 17 & 18 & 21 & 23 & 20 \\5 & 18 & 18 & 16 & 19 & 20 \\\end{bmatrix}\end{array} \)
With 5 jobs and 5 men, the stated problem is balanced.
\(\begin{array}{l}A = \begin{bmatrix}20 & 15 & 18 & 20 & 25 \\18 & 20 & 12 & 14 & 15 \\21 & 23 & 25 & 27 & 25 \\17 & 18 & 21 & 23 & 20 \\18 & 18 & 16 & 19 & 20 \\\end{bmatrix}\end{array} \)
Subtract the lowest cost element in each row from all of the elements in the given cost matrix’s row. Make sure that each row has at least one zero.
\(\begin{array}{l}A = \begin{bmatrix}5 & 0 & 3 & 5 & 10 \\6 & 8 & 0 & 2 & 3 \\0 & 2 & 4 & 6 & 4 \\0 & 1 & 4 & 6 & 3 \\2 & 2 & 0 & 3 & 4 \\\end{bmatrix}\end{array} \)
Subtract the least cost element in each Column from all of the components in the given cost matrix’s Column. Check to see if each column has at least one zero.
\(\begin{array}{l}A = \begin{bmatrix}5 & 0 & 3 & 3 & 7 \\6 & 8 & 0 & 0 & 0 \\0 & 2 & 4 & 4 & 1 \\0 & 1 & 4 & 4 & 0 \\2 & 2 & 0 & 1 & 1 \\\end{bmatrix}\end{array} \)
When the zeros are assigned, we get the following:
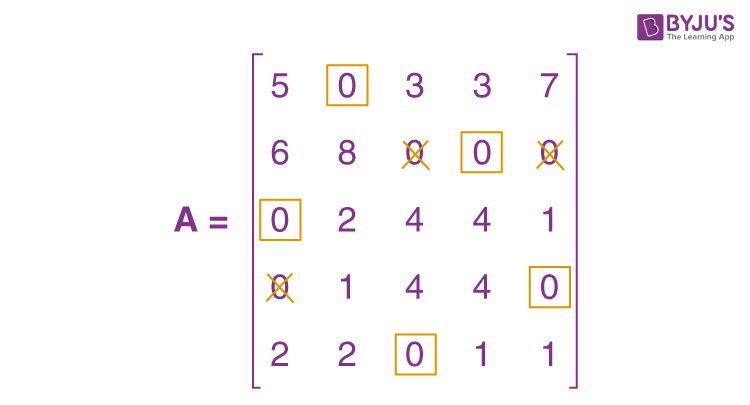
The present assignment is optimal because each row and column contain precisely one encircled zero.
Where 1 to II, 2 to IV, 3 to I, 4 to V, and 5 to III are the best assignments.
Hence, z = 15 + 14 + 21 + 20 + 16 = 86 hours is the optimal time.
Practice Question on Hungarian Method
Use the Hungarian method to solve the following assignment problem shown in table. The matrix entries represent the time it takes for each job to be processed by each machine in hours.
\(\begin{array}{l}\begin{bmatrix}J/M & I & II & III & IV & V \\1 & 9 & 22 & 58 & 11 & 19 \\2 & 43 & 78 & 72 & 50 & 63 \\3 & 41 & 28 & 91 & 37 & 45 \\4 & 74 & 42 & 27 & 49 & 39 \\5 & 36 & 11 & 57 & 22 & 25 \\\end{bmatrix}\end{array} \)
Stay tuned to BYJU’S – The Learning App and download the app to explore all Maths-related topics.
Frequently Asked Questions on Hungarian Method
What is hungarian method.
The Hungarian method is defined as a combinatorial optimization technique that solves the assignment problems in polynomial time and foreshadowed subsequent primal–dual approaches.
What are the steps involved in Hungarian method?
The following is a quick overview of the Hungarian method: Step 1: Subtract the row minima. Step 2: Subtract the column minimums. Step 3: Use a limited number of lines to cover all zeros. Step 4: Add some more zeros to the equation.
What is the purpose of the Hungarian method?
When workers are assigned to certain activities based on cost, the Hungarian method is beneficial for identifying minimum costs.
Leave a Comment Cancel reply
Your Mobile number and Email id will not be published. Required fields are marked *
Request OTP on Voice Call
Post My Comment
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.
- Practice Mathematical Algorithm
- Mathematical Algorithms
- Pythagorean Triplet
- Fibonacci Number
- Euclidean Algorithm
- LCM of Array
- GCD of Array
- Binomial Coefficient
- Catalan Numbers
- Sieve of Eratosthenes
- Euler Totient Function
- Modular Exponentiation
- Modular Multiplicative Inverse
- Stein's Algorithm
- Juggler Sequence
- Chinese Remainder Theorem
- Quiz on Fibonacci Numbers
Hungarian Algorithm for Assignment Problem | Set 1 (Introduction)
- For each row of the matrix, find the smallest element and subtract it from every element in its row.
- Do the same (as step 1) for all columns.
- Cover all zeros in the matrix using minimum number of horizontal and vertical lines.
- Test for Optimality: If the minimum number of covering lines is n, an optimal assignment is possible and we are finished. Else if lines are lesser than n, we haven’t found the optimal assignment, and must proceed to step 5.
- Determine the smallest entry not covered by any line. Subtract this entry from each uncovered row, and then add it to each covered column. Return to step 3.
Try it before moving to see the solution
Explanation for above simple example:
An example that doesn’t lead to optimal value in first attempt: In the above example, the first check for optimality did give us solution. What if we the number covering lines is less than n.
Time complexity : O(n^3), where n is the number of workers and jobs. This is because the algorithm implements the Hungarian algorithm, which is known to have a time complexity of O(n^3).
Space complexity : O(n^2), where n is the number of workers and jobs. This is because the algorithm uses a 2D cost matrix of size n x n to store the costs of assigning each worker to a job, and additional arrays of size n to store the labels, matches, and auxiliary information needed for the algorithm.
In the next post, we will be discussing implementation of the above algorithm. The implementation requires more steps as we need to find minimum number of lines to cover all 0’s using a program. References: http://www.math.harvard.edu/archive/20_spring_05/handouts/assignment_overheads.pdf https://www.youtube.com/watch?v=dQDZNHwuuOY
Similar Reads
- Mathematical
Please Login to comment...
Improve your coding skills with practice.
What kind of Experience do you want to share?

- Google OR-Tools
- Español – América Latina
- Português – Brasil
- Tiếng Việt
Solving an Assignment Problem
This section presents an example that shows how to solve an assignment problem using both the MIP solver and the CP-SAT solver.
In the example there are five workers (numbered 0-4) and four tasks (numbered 0-3). Note that there is one more worker than in the example in the Overview .
The costs of assigning workers to tasks are shown in the following table.
The problem is to assign each worker to at most one task, with no two workers performing the same task, while minimizing the total cost. Since there are more workers than tasks, one worker will not be assigned a task.
MIP solution
The following sections describe how to solve the problem using the MPSolver wrapper .
Import the libraries
The following code imports the required libraries.
Create the data
The following code creates the data for the problem.
The costs array corresponds to the table of costs for assigning workers to tasks, shown above.
Declare the MIP solver
The following code declares the MIP solver.
Create the variables
The following code creates binary integer variables for the problem.
Create the constraints
Create the objective function.
The following code creates the objective function for the problem.
The value of the objective function is the total cost over all variables that are assigned the value 1 by the solver.
Invoke the solver
The following code invokes the solver.
Print the solution
The following code prints the solution to the problem.
Here is the output of the program.
Complete programs
Here are the complete programs for the MIP solution.
CP SAT solution
The following sections describe how to solve the problem using the CP-SAT solver.
Declare the model
The following code declares the CP-SAT model.
The following code sets up the data for the problem.
The following code creates the constraints for the problem.
Here are the complete programs for the CP-SAT solution.
Except as otherwise noted, the content of this page is licensed under the Creative Commons Attribution 4.0 License , and code samples are licensed under the Apache 2.0 License . For details, see the Google Developers Site Policies . Java is a registered trademark of Oracle and/or its affiliates.
Last updated 2024-08-28 UTC.
- MapReduce Algorithm
- Linear Programming using Pyomo
- Networking and Professional Development for Machine Learning Careers in the USA
- Predicting Employee Churn in Python
- Airflow Operators

Solving Assignment Problem using Linear Programming in Python
Learn how to use Python PuLP to solve Assignment problems using Linear Programming.
In earlier articles, we have seen various applications of Linear programming such as transportation, transshipment problem, Cargo Loading problem, and shift-scheduling problem. Now In this tutorial, we will focus on another model that comes under the class of linear programming model known as the Assignment problem. Its objective function is similar to transportation problems. Here we minimize the objective function time or cost of manufacturing the products by allocating one job to one machine.
If we want to solve the maximization problem assignment problem then we subtract all the elements of the matrix from the highest element in the matrix or multiply the entire matrix by –1 and continue with the procedure. For solving the assignment problem, we use the Assignment technique or Hungarian method, or Flood’s technique.
The transportation problem is a special case of the linear programming model and the assignment problem is a special case of transportation problem, therefore it is also a special case of the linear programming problem.
In this tutorial, we are going to cover the following topics:
Assignment Problem
A problem that requires pairing two sets of items given a set of paired costs or profit in such a way that the total cost of the pairings is minimized or maximized. The assignment problem is a special case of linear programming.
For example, an operation manager needs to assign four jobs to four machines. The project manager needs to assign four projects to four staff members. Similarly, the marketing manager needs to assign the 4 salespersons to 4 territories. The manager’s goal is to minimize the total time or cost.
Problem Formulation
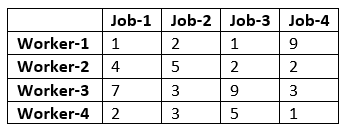
A manager has prepared a table that shows the cost of performing each of four jobs by each of four employees. The manager has stated his goal is to develop a set of job assignments that will minimize the total cost of getting all 4 jobs.
Initialize LP Model
In this step, we will import all the classes and functions of pulp module and create a Minimization LP problem using LpProblem class.
Define Decision Variable
In this step, we will define the decision variables. In our problem, we have two variable lists: workers and jobs. Let’s create them using LpVariable.dicts() class. LpVariable.dicts() used with Python’s list comprehension. LpVariable.dicts() will take the following four values:
- First, prefix name of what this variable represents.
- Second is the list of all the variables.
- Third is the lower bound on this variable.
- Fourth variable is the upper bound.
- Fourth is essentially the type of data (discrete or continuous). The options for the fourth parameter are LpContinuous or LpInteger .
Let’s first create a list route for the route between warehouse and project site and create the decision variables using LpVariable.dicts() the method.
Define Objective Function
In this step, we will define the minimum objective function by adding it to the LpProblem object. lpSum(vector)is used here to define multiple linear expressions. It also used list comprehension to add multiple variables.
Define the Constraints
Here, we are adding two types of constraints: Each job can be assigned to only one employee constraint and Each employee can be assigned to only one job. We have added the 2 constraints defined in the problem by adding them to the LpProblem object.

Solve Model
In this step, we will solve the LP problem by calling solve() method. We can print the final value by using the following for loop.
From the above results, we can infer that Worker-1 will be assigned to Job-1, Worker-2 will be assigned to job-3, Worker-3 will be assigned to Job-2, and Worker-4 will assign with job-4.
In this article, we have learned about Assignment problems, Problem Formulation, and implementation using the python PuLp library. We have solved the Assignment problem using a Linear programming problem in Python. Of course, this is just a simple case study, we can add more constraints to it and make it more complicated. You can also run other case studies on Cargo Loading problems , Staff scheduling problems . In upcoming articles, we will write more on different optimization problems such as transshipment problem, balanced diet problem. You can revise the basics of mathematical concepts in this article and learn about Linear Programming in this article .
- Solving Blending Problem in Python using Gurobi
- Transshipment Problem in Python Using PuLP
You May Also Like

Data Visualization using Seaborn

Spectral Clustering

AdaBoost Classifier in Python
Assignment Problem: Linear Programming
The assignment problem is a special type of transportation problem , where the objective is to minimize the cost or time of completing a number of jobs by a number of persons.
In other words, when the problem involves the allocation of n different facilities to n different tasks, it is often termed as an assignment problem.
The model's primary usefulness is for planning. The assignment problem also encompasses an important sub-class of so-called shortest- (or longest-) route models. The assignment model is useful in solving problems such as, assignment of machines to jobs, assignment of salesmen to sales territories, travelling salesman problem, etc.
It may be noted that with n facilities and n jobs, there are n! possible assignments. One way of finding an optimal assignment is to write all the n! possible arrangements, evaluate their total cost, and select the assignment with minimum cost. But, due to heavy computational burden this method is not suitable. This chapter concentrates on an efficient method for solving assignment problems that was developed by a Hungarian mathematician D.Konig.
"A mathematician is a device for turning coffee into theorems." -Paul Erdos
Formulation of an assignment problem
Suppose a company has n persons of different capacities available for performing each different job in the concern, and there are the same number of jobs of different types. One person can be given one and only one job. The objective of this assignment problem is to assign n persons to n jobs, so as to minimize the total assignment cost. The cost matrix for this problem is given below:
The structure of an assignment problem is identical to that of a transportation problem.
To formulate the assignment problem in mathematical programming terms , we define the activity variables as
for i = 1, 2, ..., n and j = 1, 2, ..., n
In the above table, c ij is the cost of performing jth job by ith worker.
Generalized Form of an Assignment Problem
The optimization model is
Minimize c 11 x 11 + c 12 x 12 + ------- + c nn x nn
subject to x i1 + x i2 +..........+ x in = 1 i = 1, 2,......., n x 1j + x 2j +..........+ x nj = 1 j = 1, 2,......., n
x ij = 0 or 1
In Σ Sigma notation
x ij = 0 or 1 for all i and j
An assignment problem can be solved by transportation methods, but due to high degree of degeneracy the usual computational techniques of a transportation problem become very inefficient. Therefore, a special method is available for solving such type of problems in a more efficient way.
Assumptions in Assignment Problem
- Number of jobs is equal to the number of machines or persons.
- Each man or machine is assigned only one job.
- Each man or machine is independently capable of handling any job to be done.
- Assigning criteria is clearly specified (minimizing cost or maximizing profit).
Share this article with your friends
Operations Research Simplified Back Next
Goal programming Linear programming Simplex Method Transportation Problem
Your Article Library
Assignment problem in linear programming : introduction and assignment model.
ADVERTISEMENTS:
Assignment problem is a special type of linear programming problem which deals with the allocation of the various resources to the various activities on one to one basis. It does it in such a way that the cost or time involved in the process is minimum and profit or sale is maximum. Though there problems can be solved by simplex method or by transportation method but assignment model gives a simpler approach for these problems.
In a factory, a supervisor may have six workers available and six jobs to fire. He will have to take decision regarding which job should be given to which worker. Problem forms one to one basis. This is an assignment problem.
1. Assignment Model :
Suppose there are n facilitates and n jobs it is clear that in this case, there will be n assignments. Each facility or say worker can perform each job, one at a time. But there should be certain procedure by which assignment should be made so that the profit is maximized or the cost or time is minimized.
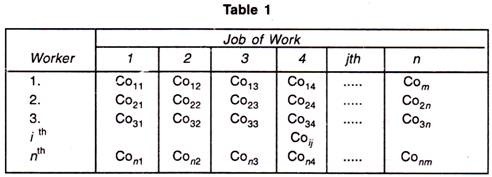
In the table, Co ij is defined as the cost when j th job is assigned to i th worker. It maybe noted here that this is a special case of transportation problem when the number of rows is equal to number of columns.
Mathematical Formulation:
Any basic feasible solution of an Assignment problem consists (2n – 1) variables of which the (n – 1) variables are zero, n is number of jobs or number of facilities. Due to this high degeneracy, if we solve the problem by usual transportation method, it will be a complex and time consuming work. Thus a separate technique is derived for it. Before going to the absolute method it is very important to formulate the problem.
Suppose x jj is a variable which is defined as
1 if the i th job is assigned to j th machine or facility
0 if the i th job is not assigned to j th machine or facility.
Now as the problem forms one to one basis or one job is to be assigned to one facility or machine.

The total assignment cost will be given by
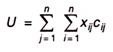
The above definition can be developed into mathematical model as follows:
Determine x ij > 0 (i, j = 1,2, 3…n) in order to
Subjected to constraints

and x ij is either zero or one.
Method to solve Problem (Hungarian Technique):
Consider the objective function of minimization type. Following steps are involved in solving this Assignment problem,
1. Locate the smallest cost element in each row of the given cost table starting with the first row. Now, this smallest element is subtracted form each element of that row. So, we will be getting at least one zero in each row of this new table.
2. Having constructed the table (as by step-1) take the columns of the table. Starting from first column locate the smallest cost element in each column. Now subtract this smallest element from each element of that column. Having performed the step 1 and step 2, we will be getting at least one zero in each column in the reduced cost table.
3. Now, the assignments are made for the reduced table in following manner.
(i) Rows are examined successively, until the row with exactly single (one) zero is found. Assignment is made to this single zero by putting square □ around it and in the corresponding column, all other zeros are crossed out (x) because these will not be used to make any other assignment in this column. Step is conducted for each row.
(ii) Step 3 (i) in now performed on the columns as follow:- columns are examined successively till a column with exactly one zero is found. Now , assignment is made to this single zero by putting the square around it and at the same time, all other zeros in the corresponding rows are crossed out (x) step is conducted for each column.
(iii) Step 3, (i) and 3 (ii) are repeated till all the zeros are either marked or crossed out. Now, if the number of marked zeros or the assignments made are equal to number of rows or columns, optimum solution has been achieved. There will be exactly single assignment in each or columns without any assignment. In this case, we will go to step 4.
4. At this stage, draw the minimum number of lines (horizontal and vertical) necessary to cover all zeros in the matrix obtained in step 3, Following procedure is adopted:
(iii) Now tick mark all the rows that are not already marked and that have assignment in the marked columns.
(iv) All the steps i.e. (4(i), 4(ii), 4(iii) are repeated until no more rows or columns can be marked.
(v) Now draw straight lines which pass through all the un marked rows and marked columns. It can also be noticed that in an n x n matrix, always less than ‘n’ lines will cover all the zeros if there is no solution among them.
5. In step 4, if the number of lines drawn are equal to n or the number of rows, then it is the optimum solution if not, then go to step 6.
6. Select the smallest element among all the uncovered elements. Now, this element is subtracted from all the uncovered elements and added to the element which lies at the intersection of two lines. This is the matrix for fresh assignments.
7. Repeat the procedure from step (3) until the number of assignments becomes equal to the number of rows or number of columns.
Related Articles:
- Two Phase Methods of Problem Solving in Linear Programming: First and Second Phase
- Linear Programming: Applications, Definitions and Problems
No comments yet.
Leave a reply click here to cancel reply..
You must be logged in to post a comment.
Procedure, Example Solved Problem | Operations Research - Solution of assignment problems (Hungarian Method) | 12th Business Maths and Statistics : Chapter 10 : Operations Research
Chapter: 12th business maths and statistics : chapter 10 : operations research.
Solution of assignment problems (Hungarian Method)
First check whether the number of rows is equal to the numbers of columns, if it is so, the assignment problem is said to be balanced.
Step :1 Choose the least element in each row and subtract it from all the elements of that row.
Step :2 Choose the least element in each column and subtract it from all the elements of that column. Step 2 has to be performed from the table obtained in step 1.
Step:3 Check whether there is atleast one zero in each row and each column and make an assignment as follows.
Step :4 If each row and each column contains exactly one assignment, then the solution is optimal.
Example 10.7
Solve the following assignment problem. Cell values represent cost of assigning job A, B, C and D to the machines I, II, III and IV.

Here the number of rows and columns are equal.
∴ The given assignment problem is balanced. Now let us find the solution.
Step 1: Select a smallest element in each row and subtract this from all the elements in its row.
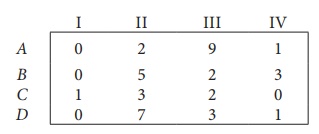
Look for atleast one zero in each row and each column.Otherwise go to step 2.
Step 2: Select the smallest element in each column and subtract this from all the elements in its column.

Since each row and column contains atleast one zero, assignments can be made.
Step 3 (Assignment):
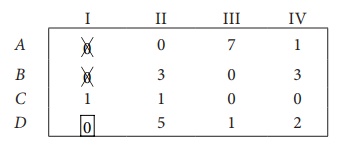
Thus all the four assignments have been made. The optimal assignment schedule and total cost is
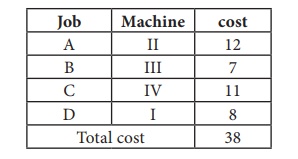
The optimal assignment (minimum) cost
Example 10.8
Consider the problem of assigning five jobs to five persons. The assignment costs are given as follows. Determine the optimum assignment schedule.
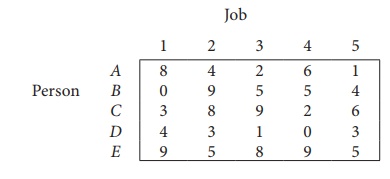
∴ The given assignment problem is balanced.
Now let us find the solution.
The cost matrix of the given assignment problem is
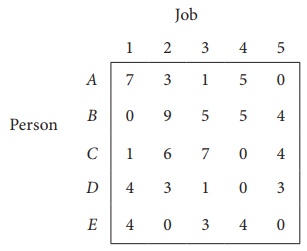
Column 3 contains no zero. Go to Step 2.

Thus all the five assignments have been made. The Optimal assignment schedule and total cost is
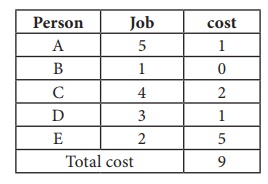
The optimal assignment (minimum) cost = ` 9
Example 10.9
Solve the following assignment problem.
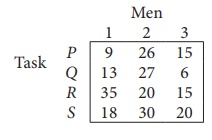
Since the number of columns is less than the number of rows, given assignment problem is unbalanced one. To balance it , introduce a dummy column with all the entries zero. The revised assignment problem is
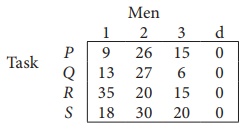
Here only 3 tasks can be assigned to 3 men.
Step 1: is not necessary, since each row contains zero entry. Go to Step 2.
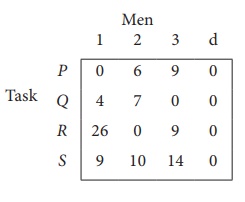
Step 3 (Assignment) :
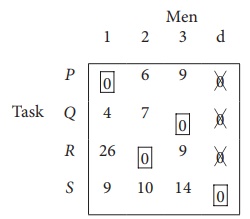
Since each row and each columncontains exactly one assignment,all the three men have been assigned a task. But task S is not assigned to any Man. The optimal assignment schedule and total cost is
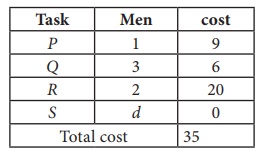
The optimal assignment (minimum) cost = ₹ 35
Related Topics
Privacy Policy , Terms and Conditions , DMCA Policy and Compliant
Copyright © 2018-2023 BrainKart.com; All Rights Reserved. Developed by Therithal info, Chennai.
Quadratic assignment problem
Author: Thomas Kueny, Eric Miller, Natasha Rice, Joseph Szczerba, David Wittmann (SysEn 5800 Fall 2020)
- 1 Introduction
- 2.1 Koopmans-Beckman Mathematical Formulation
- 2.2.1 Parameters
- 2.3.1 Optimization Problem
- 2.4 Computational Complexity
- 2.5 Algorithmic Discussions
- 2.6 Branch and Bound Procedures
- 2.7 Linearizations
- 3.1 QAP with 3 Facilities
- 4.1 Inter-plant Transportation Problem
- 4.2 The Backboard Wiring Problem
- 4.3 Hospital Layout
- 4.4 Exam Scheduling System
- 5 Conclusion
- 6 References
Introduction
The Quadratic Assignment Problem (QAP), discovered by Koopmans and Beckmann in 1957 [1] , is a mathematical optimization module created to describe the location of invisible economic activities. An NP-Complete problem, this model can be applied to many other optimization problems outside of the field of economics. It has been used to optimize backboards, inter-plant transportation, hospital transportation, exam scheduling, along with many other applications not described within this page.
Theory, Methodology, and/or Algorithmic Discussions
Koopmans-beckman mathematical formulation.
Economists Koopmans and Beckman began their investigation of the QAP to ascertain the optimal method of locating important economic resources in a given area. The Koopmans-Beckman formulation of the QAP aims to achieve the objective of assigning facilities to locations in order to minimize the overall cost. Below is the Koopmans-Beckman formulation of the QAP as described by neos-guide.org.
Quadratic Assignment Problem Formulation

Inner Product

Note: The true objective cost function only requires summing entries above the diagonal in the matrix comprised of elements

Since this matrix is symmetric with zeroes on the diagonal, dividing by 2 removes the double count of each element to give the correct cost value. See the Numerical Example section for an example of this note.
Optimization Problem
With all of this information, the QAP can be summarized as:

Computational Complexity
QAP belongs to the classification of problems known as NP-complete, thus being a computationally complex problem. QAP’s NP-completeness was proven by Sahni and Gonzalez in 1976, who states that of all combinatorial optimization problems, QAP is the “hardest of the hard”. [2]
Algorithmic Discussions
While an algorithm that can solve QAP in polynomial time is unlikely to exist, there are three primary methods for acquiring the optimal solution to a QAP problem:
- Dynamic Program
- Cutting Plane
Branch and Bound Procedures
The third method has been proven to be the most effective in solving QAP, although when n > 15, QAP begins to become virtually unsolvable.
The Branch and Bound method was first proposed by Ailsa Land and Alison Doig in 1960 and is the most commonly used tool for solving NP-hard optimization problems.
A branch-and-bound algorithm consists of a systematic enumeration of candidate solutions by means of state space search: the set of candidate solutions is thought of as forming a rooted tree with the full set at the root. The algorithm explores branches of this tree, which represent subsets of the solution set. Before one lists all of the candidate solutions of a branch, the branch is checked against upper and lower estimated bounds on the optimal solution, and the branch is eliminated if it cannot produce a better solution than the best one found so far by the algorithm.
Linearizations
The first attempts to solve the QAP eliminated the quadratic term in the objective function of

in order to transform the problem into a (mixed) 0-1 linear program. The objective function is usually linearized by introducing new variables and new linear (and binary) constraints. Then existing methods for (mixed) linear integer programming (MILP) can be applied. The very large number of new variables and constraints, however, usually poses an obstacle for efficiently solving the resulting linear integer programs. MILP formulations provide LP relaxations of the problem which can be used to compute lower bounds.
Numerical Example
Qap with 3 facilities.

Applications
Inter-plant transportation problem.
The QAP was first introduced by Koopmans and Beckmann to address how economic decisions could be made to optimize the transportation costs of goods between both manufacturing plants and locations. [1] Factoring in the location of each of the manufacturing plants as well as the volume of goods between locations to maximize revenue is what distinguishes this from other linear programming assignment problems like the Knapsack Problem.
The Backboard Wiring Problem
As the QAP is focused on minimizing the cost of traveling from one location to another, it is an ideal approach to determining the placement of components in many modern electronics. Leon Steinberg proposed a QAP solution to optimize the layout of elements on a blackboard by minimizing the total amount of wiring required. [4]
When defining the problem Steinberg states that we have a set of n elements

as well as a set of r points

In his paper he derives the below formula:

In his paper Steinberg a backboard with a 9 by 4 array, allowing for 36 potential positions for the 34 components that needed to be placed on the backboard. For the calculation, he selected a random initial placement of s1 and chose a random family of 25 unconnected sets.
The initial placement of components is shown below:

After the initial placement of elements, it took an additional 35 iterations to get us to our final optimized backboard layout. Leading to a total of 59 iterations and a final wire length of 4,969.440.
Hospital Layout
Building new hospitals was a common event in 1977 when Alealid N Elshafei wrote his paper on "Hospital Layouts as a Quadratic Assignment Problem". [5] With the high initial cost to construct the hospital and to staff it, it is important to ensure that it is operating as efficiently as possible. Elshafei's paper was commissioned to create an optimization formula to locate clinics within a building in such a way that minimizes the total distance that a patient travels within the hospital throughout the year. When doing a study of a major hospital in Cairo he determined that the Outpatient ward was acting as a bottleneck in the hospital and focused his efforts on optimizing the 17 departments there.
Elshafei identified the following QAP to determine where clinics should be placed:

For the Cairo hospital with 17 clinics, and one receiving and recording room bringing us to a total of 18 facilities. By running the above optimization Elshafei was able to get the total distance per year down to 11,281,887 from a distance of 13,973,298 based on the original hospital layout.
Exam Scheduling System
The scheduling system uses matrices for Exams, Time Slots, and Rooms with the goal of reducing the rate of schedule conflicts. To accomplish this goal, the “examination with the highest cross faculty student is been prioritized in the schedule after which the examination with the highest number of cross-program is considered and finally with the highest number of repeating student, at each stage group with the highest number of student are prioritized.” [6]

- ↑ 1.0 1.1 1.2 Koopmans, T., & Beckmann, M. (1957). Assignment Problems and the Location of Economic Activities. Econometrica, 25(1), 53-76. doi:10.2307/1907742
- ↑ 2.0 2.1 Quadratic Assignment Problem. (2020). Retrieved December 14, 2020, from https://neos-guide.org/content/quadratic-assignment-problem
- ↑ 3.0 3.1 3.2 Burkard, R. E., Çela, E., Pardalos, P. M., & Pitsoulis, L. S. (2013). The Quadratic Assignment Problem. https://www.opt.math.tugraz.at/~cela/papers/qap_bericht.pdf .
- ↑ 4.0 4.1 Leon Steinberg. The Backboard Wiring Problem: A Placement Algorithm. SIAM Review . 1961;3(1):37.
- ↑ 5.0 5.1 Alwalid N. Elshafei. Hospital Layout as a Quadratic Assignment Problem. Operational Research Quarterly (1970-1977) . 1977;28(1):167. doi:10.2307/300878
- ↑ 6.0 6.1 Muktar, D., & Ahmad, Z.M. (2014). Examination Scheduling System Based On Quadratic Assignment.
Navigation menu
Copyright © 2003 by Robert Fourer, David M. Gay and Brian W. Kernighan
Operations Research by P. Mariappan
Get full access to Operations Research and 60K+ other titles, with a free 10-day trial of O'Reilly.
There are also live events, courses curated by job role, and more.
Assignment Problem
5.1 introduction.
The assignment problem is one of the special type of transportation problem for which more efficient (less-time consuming) solution method has been devised by KUHN (1956) and FLOOD (1956). The justification of the steps leading to the solution is based on theorems proved by Hungarian mathematicians KONEIG (1950) and EGERVARY (1953), hence the method is named Hungarian.
5.2 GENERAL MODEL OF THE ASSIGNMENT PROBLEM
Consider n jobs and n persons. Assume that each job can be done only by one person and the time a person required for completing the i th job (i = 1,2,...n) by the j th person (j = 1,2,...n) is denoted by a real number C ij . On the whole this model deals with the assignment of n candidates to n jobs ...
Get Operations Research now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.
Don’t leave empty-handed
Get Mark Richards’s Software Architecture Patterns ebook to better understand how to design components—and how they should interact.
It’s yours, free.

Check it out now on O’Reilly
Dive in for free with a 10-day trial of the O’Reilly learning platform—then explore all the other resources our members count on to build skills and solve problems every day.


IMAGES
VIDEO
COMMENTS
The formal definition of the assignment problem (or linear assignment problem) is . Given two sets, A and T, together with a weight function C : A × T → R.Find a bijection f : A → T such that the cost function: (, ())is minimized. Usually the weight function is viewed as a square real-valued matrix C, so that the cost function is written down as: , The problem is "linear" because the cost ...
After reading this article you will learn about:- 1. Meaning of Assignment Problem 2. Definition of Assignment Problem 3. Mathematical Formulation 4. Hungarian Method 5. Variations. Meaning of Assignment Problem: An assignment problem is a particular case of transportation problem where the objective is to assign a number of resources to an equal number of activities so as to minimise total ...
The Hungarian method is a computational optimization technique that addresses the assignment problem in polynomial time and foreshadows following primal-dual alternatives. In 1955, Harold Kuhn used the term "Hungarian method" to honour two Hungarian mathematicians, Dénes Kőnig and Jenő Egerváry. Let's go through the steps of the Hungarian method with the help of a solved example.
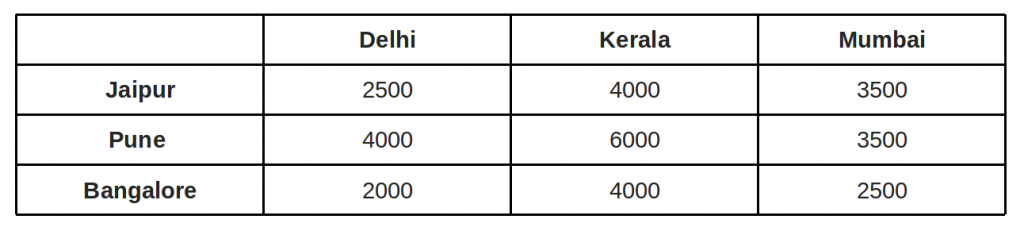
Step 3: Cover all zeroes with minimum number of. horizontal and vertical lines. Step 4: Since we need 3 lines to cover all zeroes, we have found the optimal assignment. 2500 4000 3500. 4000 6000 3500. 2000 4000 2500. So the optimal cost is 4000 + 3500 + 2000 = 9500. An example that doesn't lead to optimal value in first attempt: In the above ...
The following code prints the solution to the problem. Here is the output of the program. Total cost = 265.0. Worker 0 assigned to task 3. Cost = 70. Worker 1 assigned to task 2. Cost = 55. Worker 2 assigned to task 1. Cost = 95.
In this step, we will solve the LP problem by calling solve () method. We can print the final value by using the following for loop. From the above results, we can infer that Worker-1 will be assigned to Job-1, Worker-2 will be assigned to job-3, Worker-3 will be assigned to Job-2, and Worker-4 will assign with job-4.
302 Applications of Discrete Mathematics permutation can be generated in just 10−9 seconds, an assignment problem with n = 30 would require at least 8· 1015 years of computer time to solve by generating all 30! permutations. Therefore a better method is needed. Before developing a better algorithm, we need to set up a model for the
Assignment Problem is a special type of linear programming problem where the objective is to minimise the cost or time of completing a number of jobs by a number of persons. The assignment problem in the general form can be stated as follows: "Given n facilities, n jobs and the effectiveness of each facility for each job, the problem is to ...
Mazzola and Neebe [49] present a general model for the assignment problem with side constraints that adds the following constraint or constraints to either the classic AP model in Section 2.1 or the classic AP recognizing agent qualifications model in Section 2.2: ∑ i = 1 n ∑ j = 1 n r ijk x ijk ⩽ b k, where r ijk is the amount of ...
The assignment problem is a special type of transportation problem, ... route models. The assignment model is useful in solving problems such as, assignment of machines to jobs, assignment of salesmen to sales territories, travelling salesman problem, etc. It may be noted that with n facilities and n jobs, there are n! possible assignments. ...
The Assignment Problem: An Example A company has 4 machines available for assignment to 4 tasks. Any machine can be assigned to any task, and each task requires processing by one machine. The time required to set up each machine for the processing of each task is given in the table below. TIME (Hours) Task 1 Task 2 Task 3 Task 4 Machine 1 13 4 7 6
This is an assignment problem. 1. Assignment Model: Suppose there are n facilitates and n jobs it is clear that in this case, there will be n assignments. Each facility or say worker can perform each job, one at a time. But there should be certain procedure by which assignment should be made so that the profit is maximized or the cost or time ...
Step :4 If each row and each column contains exactly one assignment, then the solution is optimal. Example 10.7. Solve the following assignment problem. Cell values represent cost of assigning job A, B, C and D to the machines I, II, III and IV. Solution: Here the number of rows and columns are equal. ∴ The given assignment problem is ...
The Quadratic Assignment Problem (QAP), discovered by Koopmans and Beckmann in 1957, is a mathematical optimization module created to describe the location of invisible economic activities. An NP-Complete problem, this model can be applied to many other optimization problems outside of the field of economics.
Matrix model of the assignment problem. The network model is in Fig. 13. It is very similar to the transportation model except the external flows are all +1 or -1. The only relevant parameter for the assignment model is arc cost (not shown in the figure for clarity) ; all other parameters should be set to default values.
model file. Clearly we want to set up a general model to deal with this prob-lem. 3.2 An AMPL model for the transportation problem. Two fundamental sets of objects underlie the transportation problem: the sources or origins (mills, in our example) and the destinations (factories). Thus we begin the. AMPL. model with a declaration of these two sets:
Step 3. Draw lines through appropriate rows and columns so that all the zero entries of the cost matrix are covered and the minimum number of such lines is used. Step 4. Test for Optimality: (i) If the minimum number of covering lines is n, an optimal assignment of zeros is possible and we are finished.
7. Identify the relationship between assignment problems and transportation problems. 8. Formulate a spreadsheet model for an assignment problem from a description of the problem. 9. Do the same for some variants of assignment problems. 10. Give the name of an algorithm that can solve huge assignment problems that are well
We embark on an agenda to investigate how stochastic travel times and risk aversion transform the traditional traffic assignment problem and its corresponding equilibrium concepts. Moving from deterministic to stochastic travel times with risk-averse users introduces non-convexities that make the problem more difficult to analyze. For example, even computing a best response of a user to the ...
5.1 INTRODUCTION. The assignment problem is one of the special type of transportation problem for which more efficient (less-time consuming) solution method has been devised by KUHN (1956) and FLOOD (1956). The justification of the steps leading to the solution is based on theorems proved by Hungarian mathematicians KONEIG (1950) and EGERVARY ...