central angles assignment active

• Teachers Pay Teachers
• Privacy Policy

Top Central Angles and Arcs Activities!

• by [email protected]

One of the first lessons when you enter into the Circles Unit of Geometry is Central Angles. Everything that follows further on in this unit builds off this key concept, so it’s extra important to really nail it! In this article we’ll go over three activities over Central Angles and Arcs you can use in your classroom to really make sure your students are prepared and confident.

Some of these activities will utilize technology and some will strictly be paper-based! Let’s dive in!

Top Central Angles and Arcs Activities

Activity #1 – partner check practice.

When first encountering Central Angles and Arcs, students might be overwhelmed by just how many different types of problems they will be faced with. In order to combat that, there are a variety of strategies you can use. One thing that I like to do is use Partner Activities . In these kinds of activities you will partner your students up into twos and give them both a worksheet. This worksheet will be divided into “Partner A” and “Partner B”. They will each choose one column to work on. Each column has 10 different problems, but the fun part is that they should get the same answers! Let’s take a look at one!

Here you’ll see that both Partner A and Partner B both should get 120 for number 1, even though they have completely different problems! The same goes for number 2, where both students should get 70. I love these types of activities because allowing your students to work together will decrease anxiety and make even tough problems more approachable. Plus, if they don’t get the same answer, they can switch and see if they can determine their own errors instead of asking you for help! If you like how this activity looks, you can find it here . I also have a similar activity, but where students have to set up equations here !

Activity #2 – Desmos Activity Builder

Whereas our first activity was a great one for practicing skills, this activity is more of an introductory or exploratory experience! Take a look here to follow along. This is a Desmos activity, which hopefully you are familiar with! These activities are fantastic for a multitude of reasons. They allow you to monitor all students with incredible ease, they are largely self-checking, and they’re more fun than just normal old paper and pencil! Let’s take a look at what this activity specifically offers.

It starts off with some basic questions allowing students to connect prior knowledge of angles to the introductory facts of circles. These questions are also self-checking! Take a look at what happened when I tried to say that 90 degrees are in a straight angle.

It then starts to apply the idea of degrees in an angle to degrees in an arc.

It also gives tips for where you may pause the class to have a discussion!

Once the students do a little more practice it ends with a slide where students will create their own central angle, name it, and determine how many degrees their arc would be.

It even throws in a self-reflection at the end so you can determine how all the students are doing! If you like the look of it, here is another link to this activity .

Activity #3 – Blooket Gold Quest

Anytime I am going over a topic that involves questions that don’t require too much calculation to answer, I love using Blookets . Blookets are by far my favorite type of online game to use to review in class, and I’m sure your students will agree. Since Central Angles and Arcs are a concept that don’t necessarily require setting up elaborate equations to solve, I would definitely take advantage and use a Blooket to practice!

Take a look at this one . You’ll see while looking through the questions that most can be answered quickly by doing some sort of addition or subtraction using given measurements, 180, or 360.

Since these are quick questions, that means this blooket would be perfect for a Gold Quest. Gold Quest is a game mode on blooket that is always a hit in my class. Students answer questions, and when they get one right they can choose between three treasure chests. Some give gold, some subtract gold, and some even allow them to swap gold with another player!

The chaos in this mode means that no student is ever out of the hunt. This means all students will be engaged and having fun all the way up till the end! I would recommend keeping the games relatively short to keep the energy up. Here is the link again .

Well, I hope you found one or more activities that you enjoyed! As always, email me at [email protected] if you have any questions!

• Privacy Overview
• Strictly Necessary Cookies

This website uses cookies so that we can provide you with the best user experience possible. Cookie information is stored in your browser and performs functions such as recognising you when you return to our website and helping our team to understand which sections of the website you find most interesting and useful.

Strictly Necessary Cookie should be enabled at all times so that we can save your preferences for cookie settings.

If you disable this cookie, we will not be able to save your preferences. This means that every time you visit this website you will need to enable or disable cookies again.

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

In order to access this I need to be confident with:

Angles of a circle

Central angle

Here you will learn about central angles of circles, inscribed angles of circles, and the central angle theorem. You will learn how to problem solve, apply the central angle theorem to solve problems, and apply the central angle theorem to solve more difficult problems.

Students first learn about central angles in geometry and expand their knowledge as they progress through high school level math classes.

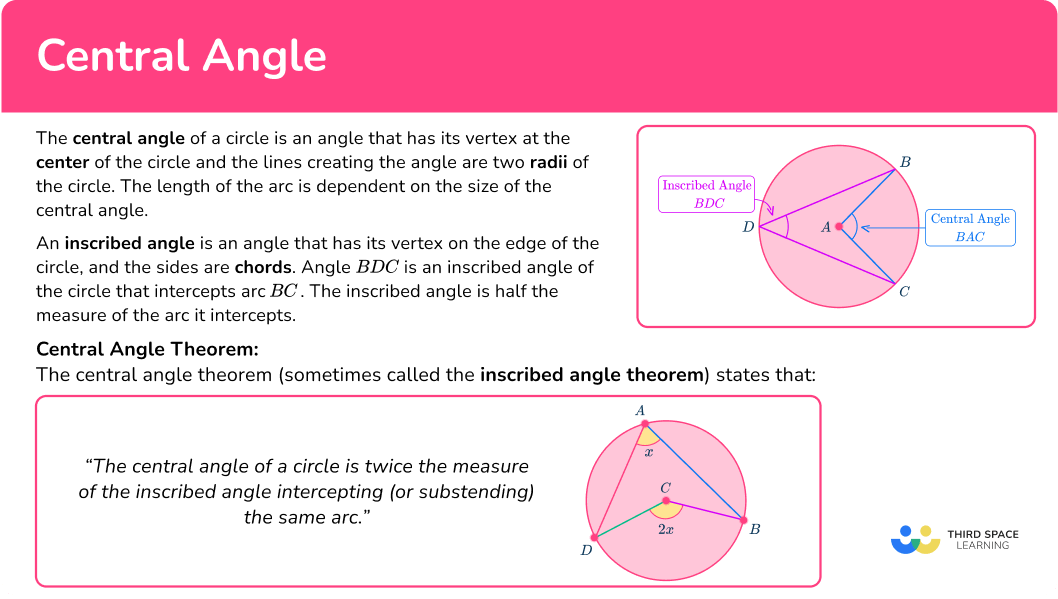
What is a central angle?

The central angle of a circle is an angle that has its vertex at the center of the circle and the lines creating the angle are two radii of the circle.

The length of the arc is dependent on the size of the central angle.

For example, in the circle below, angle BAC is a central angle because the vertex is the center of the circle with AB and AC being two radii.

The measurement of angle BAC is 90^{\circ} which means that the arc length is \cfrac{90}{360} of the circumference.

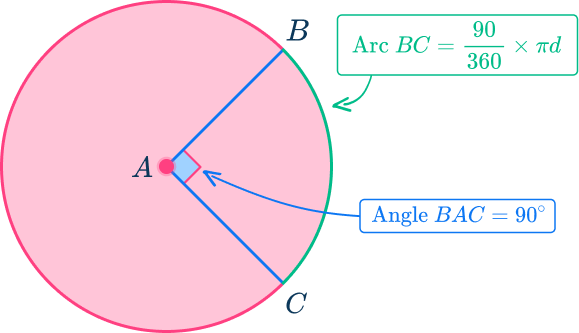
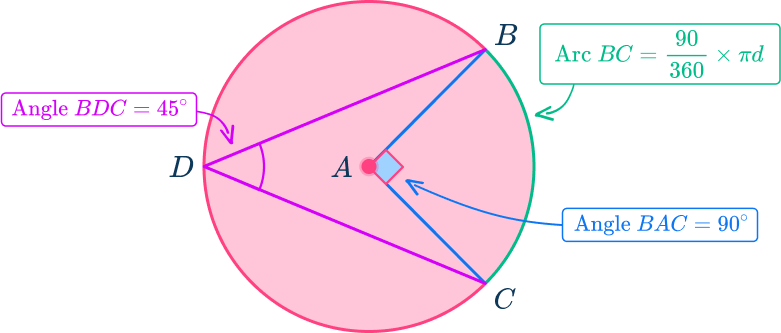
An inscribed angle is an angle that has its vertex on the edge of the circle, and the sides are chords .

Angle BDC is an inscribed angle of the circle that intercepts arc BC.

The inscribed angle is half the measure of the arc it intercepts. Continuing with the same example, the angle BDC=45^{\circ}.

[FREE] Angles Check for Understanding Quiz (Grade 4)

Use this quiz to check your grade 4 students’ understanding of angles. 10+ questions with answers covering a range of 4th grade angles topics to identify areas of strength and support!

Central angle theorem

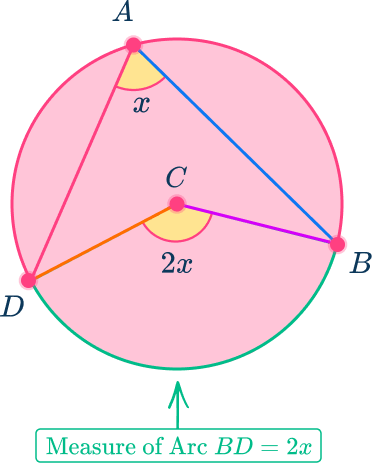
The central angle theorem (sometimes called the inscribed angle theorem ) states that:

“The central angle of a circle is twice the measure of the inscribed angle intercepting (or substending) the same arc.”

In the diagram below, angle DAB is \cfrac{1}{2} the measure of angle DCB.

Notice how both angles intercept arc DB. Arc DB is equal to the measure of angle DCB.

Before applying this theorem to problem solve, let’s look at how this relationship is always true.

The equilateral triangle ABC is inscribed in circle D. Each of the angles of the triangle are 60^{\circ}.

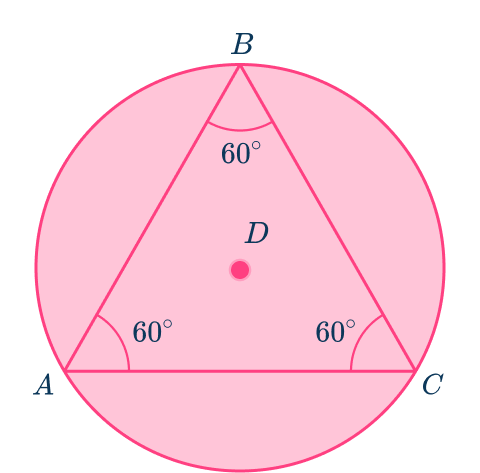
Split the equilateral triangle into three congruent isosceles triangles by connecting each vertex to the center of the circle. Now triangle ADB = triangle BDC = triangle CDA.

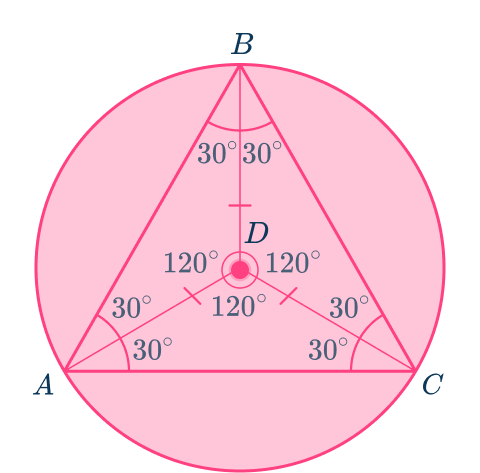
They are isosceles triangles because each of the congruent sides AD, \, BD and CD are the radii of circle D and all radii within the same circle are congruent in length.

Notice, how the vertex angles of each of the isosceles triangles have a measure of 120^{\circ} and each interior angle of the original triangle ABC is halved to 30^{\circ}.

Angle ABC is an inscribed angle that has a measure of 60^{\circ}. Angle ADC is a central angle that has a measure of 120^{\circ}.

The inscribed angle is \cfrac{1}{2} the measure of the central angle, and both angles intercept the same arc, arc AC.

This relationship is always true within any circle.

Common Core State Standards

How does this relate to high school math?

• High School Geometry – Circles: (HSG-C.A.2) Identify and describe relationships among inscribed angles, radii, and chords. Include the relationship between central, inscribed, and circumscribed angles; inscribed angles on a diameter are right angles; the radius of a circle is perpendicular to the tangent where the radius intersects the circle.

How to use central angles to solve problems

In order to use central angles to solve problems:

Identify the key parts of the circle.

Apply the central angle theorem to problem solve.

State the answer.

Central angle examples

Example 1: standard diagram inscribed angle.

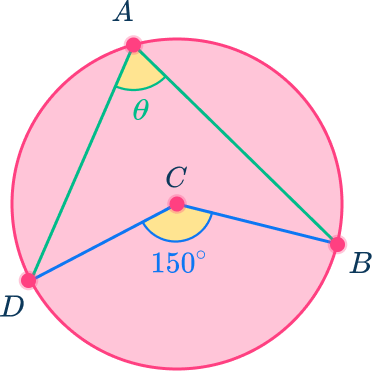
Use the diagram below to find the measure of angle BAD in circle C.

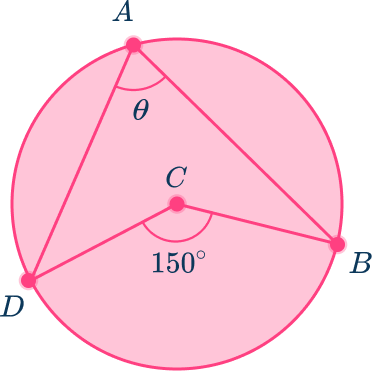
C is the center of the circle.

Angle BDC is the central angle of the circle because the vertex is at the center and the sides are the radii of the circle.

Angle BAD is the inscribed angle because the vertex is on the edge of the circle and the sides are chords.

2 Apply the central angle theorem to problem solve.

The central angle, angle BDC=150^{\circ} which means the angle it intercepts is also 150^{\circ}. Arc BD=150^{\circ}

The inscribed angle, angle BAD intercepts arc BD.

The central angle theorem states that the inscribed angle is \cfrac{1}{2} the measure of the central angle that intercepts the same arc.

So, angle BAD=\cfrac{1}{2}\times{150}=75^{\circ}.

3 State the answer.

Angle BAD=75^{\circ}

Example 2: standard diagram central angle

Use the diagram below to find the measure of the central angle, angle MLO in circle L.

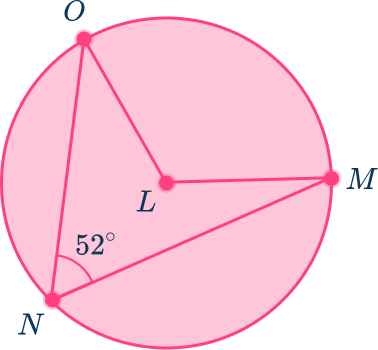
L is the center of the circle.

Angle MNO is the inscribed angle because the vertex is on the edge of the circle and the sides are chords.

Angle MLO is the central angle because the vertex is the center of the circle and the sides are the radii.

The measure of the inscribed angle is 52^{\circ}.

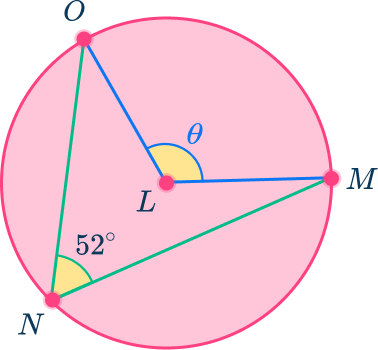
The central angle is twice the measure of the inscribed angle that intercepts the same arc.

Since the measure of the inscribed angle is 52^{\circ}, using the central angle theorem, angle OLM is 2\times{52}=104^{\circ}.

Angle MLO=104^{\circ}

Example 3: two inscribed angles

Use the diagram below to find the value of the central angle MHN.

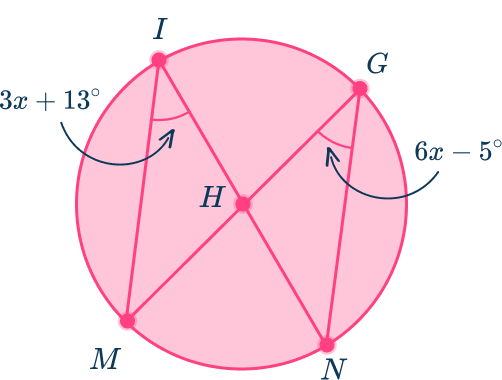
H is the center of the circle.

Angle MIN and angle MGN are inscribed angles because their vertices are on the edge of the circle and their sides are chords. They are also the same size.

Step-by-step guide: Subtended Angles in the Same Segment

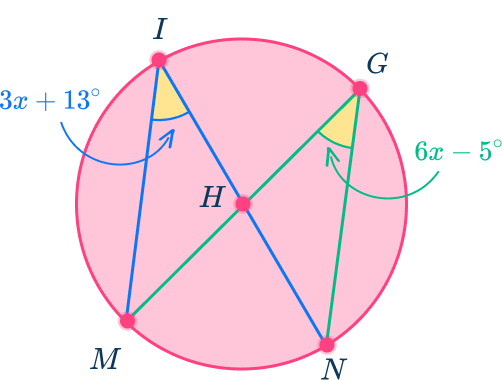
Angle MIN = angle MGN, since both inscribed angles subtend the same arc so:

Since x=6, substitute that value into either one of the expressions representing the inscribed angles to find the measure of the inscribed angles.

Angle MIN=3(6)+18=36^{\circ}

Now, Angle MIN is the inscribed angle because the vertex is on the edge of the circle and the sides are chords.

Angle MHN is the central angle because the vertex is at the center of the circle and the sides are radii.

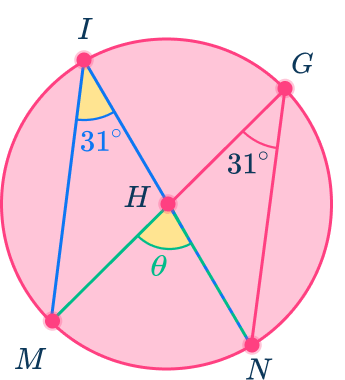
Angle MHN=2\times\text{angle}~MIN

So, angle MHN=2\times{36}=72^{\circ}.

Angle MHN=72^{\circ}

Example 4: form and solve equations using the central angle

Use the diagram below to find the measure of arc MN.

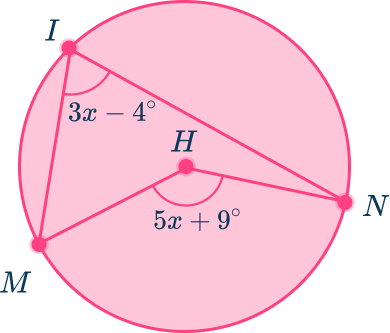
The center of the circle is H.

The central angle is angle MHN because the vertex is at the center of the circle and the sides are radii.

The inscribed angle is angle MIN because the vertex is on the edge of the circle and the sides are chords.

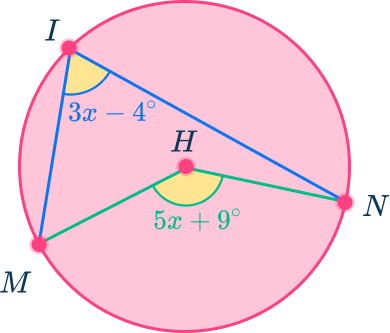
The inscribed angle is \cfrac{1}{2} the measure of the central angle that intercepts the same arc. So, in this case \text{angle}~MIN=\cfrac{1}{2}\text{ (angle}~MHN).

Substituting in the algebraic expressions, the equation is:

Substitute the value of x back into the algebraic expression for MHN to find the measure of arc MN.

Angle MHN=5x+9=5\times{17}+9=94^{\circ}

The measure of arc MN=94^{\circ}

Example 5: using triangles to find central angle

Use the diagram below to find the value of the central angle, \theta (Angle BCD ).

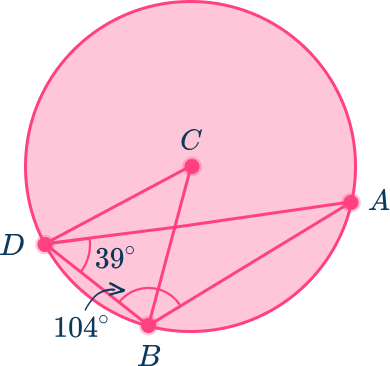
The center of the circle is C.

The central angle is angle BCD because the vertex is at the center of the circle and the sides are radii.

Angle BAD is an inscribed angle because the vertex is on the edge of the circle and the sides are chords.

Triangle ABD is an inscribed triangle because the vertices of the triangle are on the edge of the circle.

To find the central angle, first you need to know the inscribed angle BAD.

As the inscribed angle is part of a triangle, use the angle fact “the sum of angles in a triangle is 180^{\circ} to find the angle.

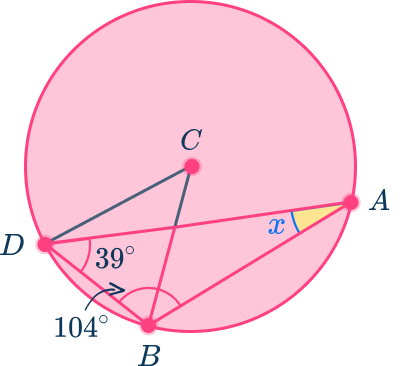
x=180-(39+104)=37^{\circ}

Now, Angle BAD is the inscribed angle because the vertex is on the edge of the circle and the sides are chords.

Angle BCD is the central angle because the vertex is at the center of the circle and the sides are radii.

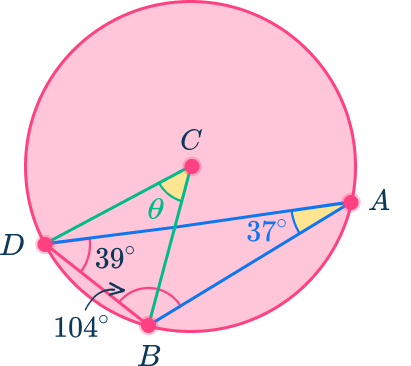
Angle BAD is \cfrac{1}{2} the measure of the central angle that intercepts the same arc, so:

\text{angle}~BAD=\cfrac{1}{2}\times\text{angle}~BCD.

Substitute in the value for angle BAD .

The central angle BCD=74^{\circ}

Example 6: right triangles

Use the diagram below to find the value of angle XWV.

Y is the center of the circle.

Angle XWV is the inscribed angle because the vertex is on the edge of the circle and the sides are chords.

Straight line, XV, is the diameter of the circle because it is a chord that goes through the center of the circle.

Angle XYV is the central angle which is also a straight angle =180^{\circ}.

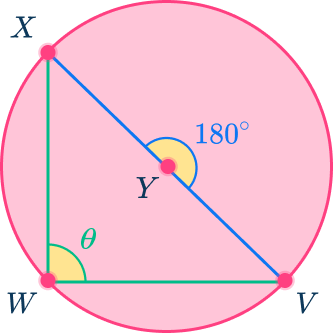
Angle XYV=180^{\circ} because it is a straight angle and it also can be considered the diameter, which intercepts the semi-circle. The measure of arc XV, is equal to 180^{\circ}.

The inscribed angle XWV intercepts the semi-circle so it is \cfrac{1}{2} the measurement of the central angle that intercepts the same arc.

Angle XWV=\cfrac{1}{2} \, (180)=90^{\circ}

Angle XWV=90^{\circ}

Example 7: arcs and angles

Use the diagram below to find the measure of the inscribed angle RTS and the central angle, RQS of circle Q.

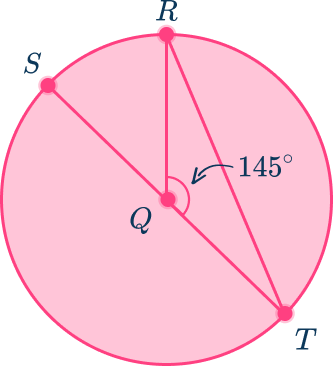
Q is the center of the circle.

Angle RTS is the inscribed angle because the vertex is on the edge of the circle and the sides are chords.

Angle SQR is the central angle because the vertex is at the center of the circle and the sides are radii.

ST is the diameter because it is a chord that goes through the center of the circle.

Angle RQT and the measure of semi-circle SRT is 180^{\circ}, so the measure of arc SR=180-145=35^{\circ}.

Arc SR is intercepted by the central angle SQR so the measurement of arc SR is equal to the measurement of central angle SQR.

\text{Arc}~SR=35^{\circ}=\text{angle}~SQR

Inscribed angle STR intercepts the same arc as central angle SQR. So, inscribed angle STR is \cfrac{1}{2} the measurement of central angle SQR.

Angle STR=\cfrac{1}{2} \times 35^{\circ}=17.5^{\circ}

Angle SQR=35^{\circ}

Angle STR=17.5^{\circ}

Teaching tips for central angles

• Have students discover the relationship between central angles and inscribed angles as well as the central angle theorem by doing hands-on constructions and measuring the relationships between the angles.
• Instead of practice problem worksheets, have students game play to practice skills.

Easy mistakes to make

• Halving and doubling incorrectly Similar to the previous misconception, the central angle is incorrectly doubled to calculate the inscribed angle whereas it should be halved.

Related circle theorem lesson

• Circle theorems
• Chords of a circle
• Tangent of a circle
• Circle chord theorems

Central angle practice problems

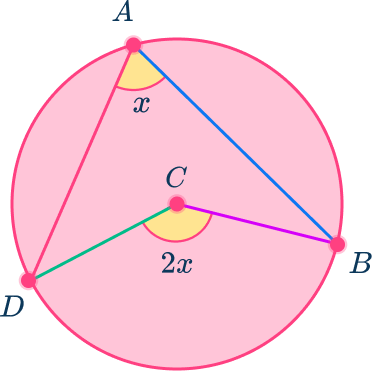
1. Find the measure of theta, \theta, angle ABC in circle B.

Angle ABC is a central angle because the vertex is at the center of a circle with the sides being radii.

Angle ADC is an inscribed angle with vertex on the edge of the circle intercepting the same arc as angle ABC.

Using the central angle theorem, angle ABC is double the measure of angle ABC.

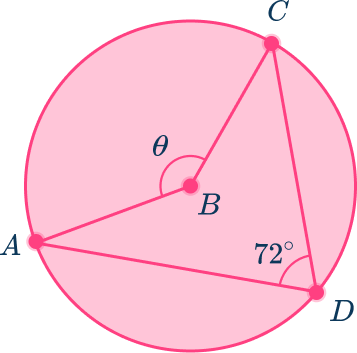
2. Find the measure of \theta, angle CBA, in circle D.

Angle ADC is a central angle because the vertex is at the center of the circle and the sides are radii.

Angle ABC is an inscribed angle because the vertex is on the edge of the circle and the sides are chords.

The central angle ADC=118^{\circ} and the inscribed angle ABC is half the measurement of angle ADC because they both intercept the same arc.

3. ABCD is a cyclic quadrilateral. Find the measure of theta, \theta, which is the reflex angle at E in circle E.

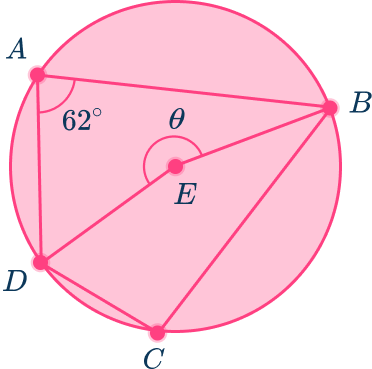
Angle BED is a central angle because the vertex is at the center of the circle and the sides are radii.

Angle BAD=62^{\circ} which means that angle BED is double angle BAD because the central angle is 2 times the inscribed angle that intercepts the same arc.

Angle BED=2\times{62}=144^{\circ}

The sum of angles at a point is 360^{\circ} so the reflex angle at E which is \theta is equal to 360-144=236^{\circ}.

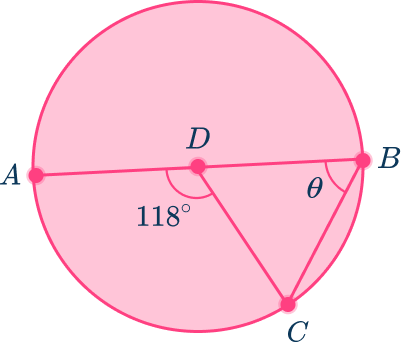
4. Find the measure of angle STR in circle Q.

Angle SQR is a central angle because the vertex is at the center of the circle and the sides are radii.

Angle STR is an inscribed angle because the vertex is on the edge of the circle with the sides being chords.

The minor arc measurement, arc RT=132^{\circ} and the measurement of semi-circle ST=180^{\circ} so arc SR=180-132=48^{\circ}.

The measure of the intercepted arc is equal to the measure of the central angle.

Arc SR=48^{\circ} which means that central angle SQR=48^{\circ} and inscribed angle STR is half the angle SQR.

5. Find the central angle measure, angle MHN, in circle H.

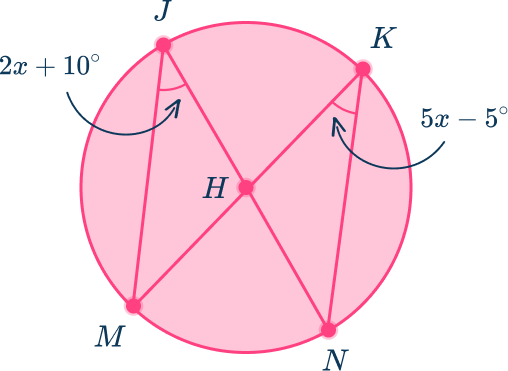
Angle MJN and angle MKN are both inscribed angles and intercept the same arc. So, they are both equal to each other.

The measure of the intercepted arc in this case is equal to the central angle measurement.

In order to find the measure of the central angle, angle MHN, you must first solve for x.

Substitute the value of x back into one of the algebraic expressions for the inscribed angle to find the measurement of the angle.

Angle MJN=2x+10=2(5)+10=20^{\circ}

The central angle is 2 times the measure of the inscribed angle that intercepts the same arc.

6. Find the measure of \theta which is the inscribed angle BAD of circle D.

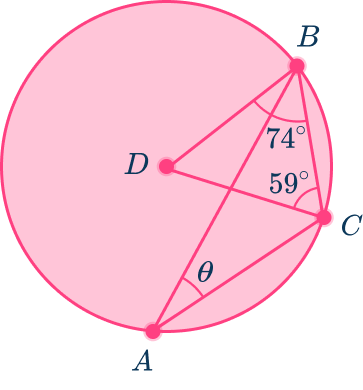
Angle BDC is a central angle of circle D because the vertex is at the center of the circle and the sides are radii.

Angle BAC is an inscribed angle because the vertex is on the edge of the circle and the sides are chords.

Triangle BCD has interior angles that sum to 180^{\circ}.

So, to find the central angle, angle BDC, subtract 59^{\circ} and 74^{\circ} from 180^{\circ}.

The inscribed angle is \cfrac{1}{2} the measure of the central angle that intercepts the same arc.

Angle BAC=\cfrac{1}{2}\times{47}=23.5^{\circ}

Central angle FAQs

A major arc is an arc that has a measure between 180^{\circ} and 360^{\circ}. A minor arc is an arc that has a measure between 0^{\circ} and 180^{\circ}.

Arc length is part of the circumference of the circle. The circumference of the circle is the distance around the circle so the length of the arc is a portion of the circumference of a circle.

Radians are a unit of measure for an angle. Typically, in trigonometry, angle measures will be expressed in radians.

Congruent arcs are arcs that have the same length and the same measurement. If the inscribed angles of a circle are congruent and intercept arcs, those arcs will be congruent.

Secants are lines that intersect a circle at two points of intersection. Chords are line segments that are created by secant lines.

The next lessons are

• Prism shape
• Types of data
• Averages and range
• Representing data

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .

[FREE] Common Core Practice Tests (3rd to 8th Grade)

Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.

Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!

Privacy Overview

Central Angles and Arcs

Related Topics: More Lessons for Grade 9 Math Math Worksheets

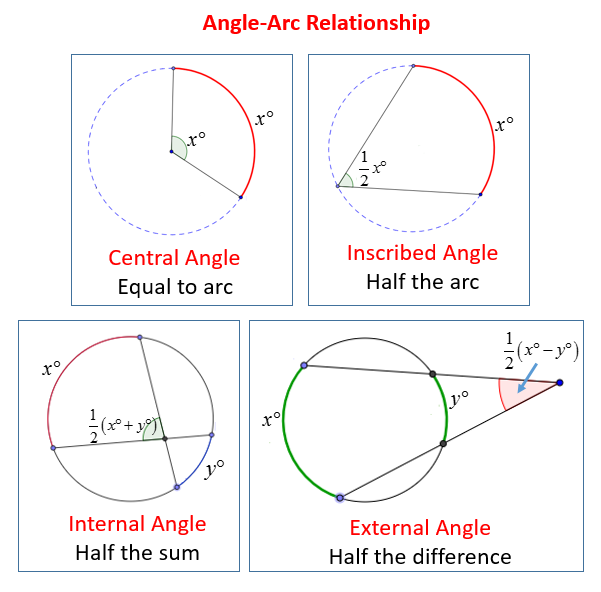
Arcs and Central Angles Students learn the definition of a central angle, and that the measure of a central angle is equal to the measure of its intercepted arc.

This video gives an introduction into central angles, circle arcs, and angle measurement. It explains the difference between a major arc and a minor arc. A central angle always form a minor arc which is less than 180 degrees in angle measure. The major arc is greater than 180 degrees. A semicircle has an intercepted arc of exactly 180 degrees. It contains plenty of examples and practice problems.

How to Find a Central Angle When Given a Radius and a Tangent?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.