
Data & Finance for Work & Life


Data Analysis: Types, Methods & Techniques (a Complete List)
( Updated Version )
While the term sounds intimidating, “data analysis” is nothing more than making sense of information in a table. It consists of filtering, sorting, grouping, and manipulating data tables with basic algebra and statistics.
In fact, you don’t need experience to understand the basics. You have already worked with data extensively in your life, and “analysis” is nothing more than a fancy word for good sense and basic logic.
Over time, people have intuitively categorized the best logical practices for treating data. These categories are what we call today types , methods , and techniques .
This article provides a comprehensive list of types, methods, and techniques, and explains the difference between them.
For a practical intro to data analysis (including types, methods, & techniques), check out our Intro to Data Analysis eBook for free.
Descriptive, Diagnostic, Predictive, & Prescriptive Analysis
If you Google “types of data analysis,” the first few results will explore descriptive , diagnostic , predictive , and prescriptive analysis. Why? Because these names are easy to understand and are used a lot in “the real world.”
Descriptive analysis is an informational method, diagnostic analysis explains “why” a phenomenon occurs, predictive analysis seeks to forecast the result of an action, and prescriptive analysis identifies solutions to a specific problem.
That said, these are only four branches of a larger analytical tree.
Good data analysts know how to position these four types within other analytical methods and tactics, allowing them to leverage strengths and weaknesses in each to uproot the most valuable insights.
Let’s explore the full analytical tree to understand how to appropriately assess and apply these four traditional types.
Tree diagram of Data Analysis Types, Methods, and Techniques
Here’s a picture to visualize the structure and hierarchy of data analysis types, methods, and techniques.
If it’s too small you can view the picture in a new tab . Open it to follow along!

Note: basic descriptive statistics such as mean , median , and mode , as well as standard deviation , are not shown because most people are already familiar with them. In the diagram, they would fall under the “descriptive” analysis type.
Tree Diagram Explained
The highest-level classification of data analysis is quantitative vs qualitative . Quantitative implies numbers while qualitative implies information other than numbers.
Quantitative data analysis then splits into mathematical analysis and artificial intelligence (AI) analysis . Mathematical types then branch into descriptive , diagnostic , predictive , and prescriptive .
Methods falling under mathematical analysis include clustering , classification , forecasting , and optimization . Qualitative data analysis methods include content analysis , narrative analysis , discourse analysis , framework analysis , and/or grounded theory .
Moreover, mathematical techniques include regression , Nïave Bayes , Simple Exponential Smoothing , cohorts , factors , linear discriminants , and more, whereas techniques falling under the AI type include artificial neural networks , decision trees , evolutionary programming , and fuzzy logic . Techniques under qualitative analysis include text analysis , coding , idea pattern analysis , and word frequency .
It’s a lot to remember! Don’t worry, once you understand the relationship and motive behind all these terms, it’ll be like riding a bike.
We’ll move down the list from top to bottom and I encourage you to open the tree diagram above in a new tab so you can follow along .
But first, let’s just address the elephant in the room: what’s the difference between methods and techniques anyway?
Difference between methods and techniques
Though often used interchangeably, methods ands techniques are not the same. By definition, methods are the process by which techniques are applied, and techniques are the practical application of those methods.
For example, consider driving. Methods include staying in your lane, stopping at a red light, and parking in a spot. Techniques include turning the steering wheel, braking, and pushing the gas pedal.
Data sets: observations and fields
It’s important to understand the basic structure of data tables to comprehend the rest of the article. A data set consists of one far-left column containing observations, then a series of columns containing the fields (aka “traits” or “characteristics”) that describe each observations. For example, imagine we want a data table for fruit. It might look like this:
| The fruit (observation) | (field1) | Avg. diameter (field 2) | Avg. time to eat (field 3) |
|---|---|---|---|
| Watermelon | 20 lbs (9 kg) | 16 inch (40 cm) | 20 minutes |
| Apple | .33 lbs (.15 kg) | 4 inch (8 cm) | 5 minutes |
| Orange | .30 lbs (.14 kg) | 4 inch (8 cm) | 5 minutes |
Now let’s turn to types, methods, and techniques. Each heading below consists of a description, relative importance, the nature of data it explores, and the motivation for using it.
Quantitative Analysis
- It accounts for more than 50% of all data analysis and is by far the most widespread and well-known type of data analysis.
- As you have seen, it holds descriptive, diagnostic, predictive, and prescriptive methods, which in turn hold some of the most important techniques available today, such as clustering and forecasting.
- It can be broken down into mathematical and AI analysis.
- Importance : Very high . Quantitative analysis is a must for anyone interesting in becoming or improving as a data analyst.
- Nature of Data: data treated under quantitative analysis is, quite simply, quantitative. It encompasses all numeric data.
- Motive: to extract insights. (Note: we’re at the top of the pyramid, this gets more insightful as we move down.)
Qualitative Analysis
- It accounts for less than 30% of all data analysis and is common in social sciences .
- It can refer to the simple recognition of qualitative elements, which is not analytic in any way, but most often refers to methods that assign numeric values to non-numeric data for analysis.
- Because of this, some argue that it’s ultimately a quantitative type.
- Importance: Medium. In general, knowing qualitative data analysis is not common or even necessary for corporate roles. However, for researchers working in social sciences, its importance is very high .
- Nature of Data: data treated under qualitative analysis is non-numeric. However, as part of the analysis, analysts turn non-numeric data into numbers, at which point many argue it is no longer qualitative analysis.
- Motive: to extract insights. (This will be more important as we move down the pyramid.)
Mathematical Analysis
- Description: mathematical data analysis is a subtype of qualitative data analysis that designates methods and techniques based on statistics, algebra, and logical reasoning to extract insights. It stands in opposition to artificial intelligence analysis.
- Importance: Very High. The most widespread methods and techniques fall under mathematical analysis. In fact, it’s so common that many people use “quantitative” and “mathematical” analysis interchangeably.
- Nature of Data: numeric. By definition, all data under mathematical analysis are numbers.
- Motive: to extract measurable insights that can be used to act upon.
Artificial Intelligence & Machine Learning Analysis
- Description: artificial intelligence and machine learning analyses designate techniques based on the titular skills. They are not traditionally mathematical, but they are quantitative since they use numbers. Applications of AI & ML analysis techniques are developing, but they’re not yet mainstream enough to show promise across the field.
- Importance: Medium . As of today (September 2020), you don’t need to be fluent in AI & ML data analysis to be a great analyst. BUT, if it’s a field that interests you, learn it. Many believe that in 10 year’s time its importance will be very high .
- Nature of Data: numeric.
- Motive: to create calculations that build on themselves in order and extract insights without direct input from a human.
Descriptive Analysis
- Description: descriptive analysis is a subtype of mathematical data analysis that uses methods and techniques to provide information about the size, dispersion, groupings, and behavior of data sets. This may sounds complicated, but just think about mean, median, and mode: all three are types of descriptive analysis. They provide information about the data set. We’ll look at specific techniques below.
- Importance: Very high. Descriptive analysis is among the most commonly used data analyses in both corporations and research today.
- Nature of Data: the nature of data under descriptive statistics is sets. A set is simply a collection of numbers that behaves in predictable ways. Data reflects real life, and there are patterns everywhere to be found. Descriptive analysis describes those patterns.
- Motive: the motive behind descriptive analysis is to understand how numbers in a set group together, how far apart they are from each other, and how often they occur. As with most statistical analysis, the more data points there are, the easier it is to describe the set.
Diagnostic Analysis
- Description: diagnostic analysis answers the question “why did it happen?” It is an advanced type of mathematical data analysis that manipulates multiple techniques, but does not own any single one. Analysts engage in diagnostic analysis when they try to explain why.
- Importance: Very high. Diagnostics are probably the most important type of data analysis for people who don’t do analysis because they’re valuable to anyone who’s curious. They’re most common in corporations, as managers often only want to know the “why.”
- Nature of Data : data under diagnostic analysis are data sets. These sets in themselves are not enough under diagnostic analysis. Instead, the analyst must know what’s behind the numbers in order to explain “why.” That’s what makes diagnostics so challenging yet so valuable.
- Motive: the motive behind diagnostics is to diagnose — to understand why.
Predictive Analysis
- Description: predictive analysis uses past data to project future data. It’s very often one of the first kinds of analysis new researchers and corporate analysts use because it is intuitive. It is a subtype of the mathematical type of data analysis, and its three notable techniques are regression, moving average, and exponential smoothing.
- Importance: Very high. Predictive analysis is critical for any data analyst working in a corporate environment. Companies always want to know what the future will hold — especially for their revenue.
- Nature of Data: Because past and future imply time, predictive data always includes an element of time. Whether it’s minutes, hours, days, months, or years, we call this time series data . In fact, this data is so important that I’ll mention it twice so you don’t forget: predictive analysis uses time series data .
- Motive: the motive for investigating time series data with predictive analysis is to predict the future in the most analytical way possible.
Prescriptive Analysis
- Description: prescriptive analysis is a subtype of mathematical analysis that answers the question “what will happen if we do X?” It’s largely underestimated in the data analysis world because it requires diagnostic and descriptive analyses to be done before it even starts. More than simple predictive analysis, prescriptive analysis builds entire data models to show how a simple change could impact the ensemble.
- Importance: High. Prescriptive analysis is most common under the finance function in many companies. Financial analysts use it to build a financial model of the financial statements that show how that data will change given alternative inputs.
- Nature of Data: the nature of data in prescriptive analysis is data sets. These data sets contain patterns that respond differently to various inputs. Data that is useful for prescriptive analysis contains correlations between different variables. It’s through these correlations that we establish patterns and prescribe action on this basis. This analysis cannot be performed on data that exists in a vacuum — it must be viewed on the backdrop of the tangibles behind it.
- Motive: the motive for prescriptive analysis is to establish, with an acceptable degree of certainty, what results we can expect given a certain action. As you might expect, this necessitates that the analyst or researcher be aware of the world behind the data, not just the data itself.
Clustering Method
- Description: the clustering method groups data points together based on their relativeness closeness to further explore and treat them based on these groupings. There are two ways to group clusters: intuitively and statistically (or K-means).
- Importance: Very high. Though most corporate roles group clusters intuitively based on management criteria, a solid understanding of how to group them mathematically is an excellent descriptive and diagnostic approach to allow for prescriptive analysis thereafter.
- Nature of Data : the nature of data useful for clustering is sets with 1 or more data fields. While most people are used to looking at only two dimensions (x and y), clustering becomes more accurate the more fields there are.
- Motive: the motive for clustering is to understand how data sets group and to explore them further based on those groups.
- Here’s an example set:

Classification Method
- Description: the classification method aims to separate and group data points based on common characteristics . This can be done intuitively or statistically.
- Importance: High. While simple on the surface, classification can become quite complex. It’s very valuable in corporate and research environments, but can feel like its not worth the work. A good analyst can execute it quickly to deliver results.
- Nature of Data: the nature of data useful for classification is data sets. As we will see, it can be used on qualitative data as well as quantitative. This method requires knowledge of the substance behind the data, not just the numbers themselves.
- Motive: the motive for classification is group data not based on mathematical relationships (which would be clustering), but by predetermined outputs. This is why it’s less useful for diagnostic analysis, and more useful for prescriptive analysis.
Forecasting Method
- Description: the forecasting method uses time past series data to forecast the future.
- Importance: Very high. Forecasting falls under predictive analysis and is arguably the most common and most important method in the corporate world. It is less useful in research, which prefers to understand the known rather than speculate about the future.
- Nature of Data: data useful for forecasting is time series data, which, as we’ve noted, always includes a variable of time.
- Motive: the motive for the forecasting method is the same as that of prescriptive analysis: the confidently estimate future values.
Optimization Method
- Description: the optimization method maximized or minimizes values in a set given a set of criteria. It is arguably most common in prescriptive analysis. In mathematical terms, it is maximizing or minimizing a function given certain constraints.
- Importance: Very high. The idea of optimization applies to more analysis types than any other method. In fact, some argue that it is the fundamental driver behind data analysis. You would use it everywhere in research and in a corporation.
- Nature of Data: the nature of optimizable data is a data set of at least two points.
- Motive: the motive behind optimization is to achieve the best result possible given certain conditions.
Content Analysis Method
- Description: content analysis is a method of qualitative analysis that quantifies textual data to track themes across a document. It’s most common in academic fields and in social sciences, where written content is the subject of inquiry.
- Importance: High. In a corporate setting, content analysis as such is less common. If anything Nïave Bayes (a technique we’ll look at below) is the closest corporations come to text. However, it is of the utmost importance for researchers. If you’re a researcher, check out this article on content analysis .
- Nature of Data: data useful for content analysis is textual data.
- Motive: the motive behind content analysis is to understand themes expressed in a large text
Narrative Analysis Method
- Description: narrative analysis is a method of qualitative analysis that quantifies stories to trace themes in them. It’s differs from content analysis because it focuses on stories rather than research documents, and the techniques used are slightly different from those in content analysis (very nuances and outside the scope of this article).
- Importance: Low. Unless you are highly specialized in working with stories, narrative analysis rare.
- Nature of Data: the nature of the data useful for the narrative analysis method is narrative text.
- Motive: the motive for narrative analysis is to uncover hidden patterns in narrative text.
Discourse Analysis Method
- Description: the discourse analysis method falls under qualitative analysis and uses thematic coding to trace patterns in real-life discourse. That said, real-life discourse is oral, so it must first be transcribed into text.
- Importance: Low. Unless you are focused on understand real-world idea sharing in a research setting, this kind of analysis is less common than the others on this list.
- Nature of Data: the nature of data useful in discourse analysis is first audio files, then transcriptions of those audio files.
- Motive: the motive behind discourse analysis is to trace patterns of real-world discussions. (As a spooky sidenote, have you ever felt like your phone microphone was listening to you and making reading suggestions? If it was, the method was discourse analysis.)
Framework Analysis Method
- Description: the framework analysis method falls under qualitative analysis and uses similar thematic coding techniques to content analysis. However, where content analysis aims to discover themes, framework analysis starts with a framework and only considers elements that fall in its purview.
- Importance: Low. As with the other textual analysis methods, framework analysis is less common in corporate settings. Even in the world of research, only some use it. Strangely, it’s very common for legislative and political research.
- Nature of Data: the nature of data useful for framework analysis is textual.
- Motive: the motive behind framework analysis is to understand what themes and parts of a text match your search criteria.
Grounded Theory Method
- Description: the grounded theory method falls under qualitative analysis and uses thematic coding to build theories around those themes.
- Importance: Low. Like other qualitative analysis techniques, grounded theory is less common in the corporate world. Even among researchers, you would be hard pressed to find many using it. Though powerful, it’s simply too rare to spend time learning.
- Nature of Data: the nature of data useful in the grounded theory method is textual.
- Motive: the motive of grounded theory method is to establish a series of theories based on themes uncovered from a text.
Clustering Technique: K-Means
- Description: k-means is a clustering technique in which data points are grouped in clusters that have the closest means. Though not considered AI or ML, it inherently requires the use of supervised learning to reevaluate clusters as data points are added. Clustering techniques can be used in diagnostic, descriptive, & prescriptive data analyses.
- Importance: Very important. If you only take 3 things from this article, k-means clustering should be part of it. It is useful in any situation where n observations have multiple characteristics and we want to put them in groups.
- Nature of Data: the nature of data is at least one characteristic per observation, but the more the merrier.
- Motive: the motive for clustering techniques such as k-means is to group observations together and either understand or react to them.
Regression Technique
- Description: simple and multivariable regressions use either one independent variable or combination of multiple independent variables to calculate a correlation to a single dependent variable using constants. Regressions are almost synonymous with correlation today.
- Importance: Very high. Along with clustering, if you only take 3 things from this article, regression techniques should be part of it. They’re everywhere in corporate and research fields alike.
- Nature of Data: the nature of data used is regressions is data sets with “n” number of observations and as many variables as are reasonable. It’s important, however, to distinguish between time series data and regression data. You cannot use regressions or time series data without accounting for time. The easier way is to use techniques under the forecasting method.
- Motive: The motive behind regression techniques is to understand correlations between independent variable(s) and a dependent one.
Nïave Bayes Technique
- Description: Nïave Bayes is a classification technique that uses simple probability to classify items based previous classifications. In plain English, the formula would be “the chance that thing with trait x belongs to class c depends on (=) the overall chance of trait x belonging to class c, multiplied by the overall chance of class c, divided by the overall chance of getting trait x.” As a formula, it’s P(c|x) = P(x|c) * P(c) / P(x).
- Importance: High. Nïave Bayes is a very common, simplistic classification techniques because it’s effective with large data sets and it can be applied to any instant in which there is a class. Google, for example, might use it to group webpages into groups for certain search engine queries.
- Nature of Data: the nature of data for Nïave Bayes is at least one class and at least two traits in a data set.
- Motive: the motive behind Nïave Bayes is to classify observations based on previous data. It’s thus considered part of predictive analysis.
Cohorts Technique
- Description: cohorts technique is a type of clustering method used in behavioral sciences to separate users by common traits. As with clustering, it can be done intuitively or mathematically, the latter of which would simply be k-means.
- Importance: Very high. With regard to resembles k-means, the cohort technique is more of a high-level counterpart. In fact, most people are familiar with it as a part of Google Analytics. It’s most common in marketing departments in corporations, rather than in research.
- Nature of Data: the nature of cohort data is data sets in which users are the observation and other fields are used as defining traits for each cohort.
- Motive: the motive for cohort analysis techniques is to group similar users and analyze how you retain them and how the churn.
Factor Technique
- Description: the factor analysis technique is a way of grouping many traits into a single factor to expedite analysis. For example, factors can be used as traits for Nïave Bayes classifications instead of more general fields.
- Importance: High. While not commonly employed in corporations, factor analysis is hugely valuable. Good data analysts use it to simplify their projects and communicate them more clearly.
- Nature of Data: the nature of data useful in factor analysis techniques is data sets with a large number of fields on its observations.
- Motive: the motive for using factor analysis techniques is to reduce the number of fields in order to more quickly analyze and communicate findings.
Linear Discriminants Technique
- Description: linear discriminant analysis techniques are similar to regressions in that they use one or more independent variable to determine a dependent variable; however, the linear discriminant technique falls under a classifier method since it uses traits as independent variables and class as a dependent variable. In this way, it becomes a classifying method AND a predictive method.
- Importance: High. Though the analyst world speaks of and uses linear discriminants less commonly, it’s a highly valuable technique to keep in mind as you progress in data analysis.
- Nature of Data: the nature of data useful for the linear discriminant technique is data sets with many fields.
- Motive: the motive for using linear discriminants is to classify observations that would be otherwise too complex for simple techniques like Nïave Bayes.
Exponential Smoothing Technique
- Description: exponential smoothing is a technique falling under the forecasting method that uses a smoothing factor on prior data in order to predict future values. It can be linear or adjusted for seasonality. The basic principle behind exponential smoothing is to use a percent weight (value between 0 and 1 called alpha) on more recent values in a series and a smaller percent weight on less recent values. The formula is f(x) = current period value * alpha + previous period value * 1-alpha.
- Importance: High. Most analysts still use the moving average technique (covered next) for forecasting, though it is less efficient than exponential moving, because it’s easy to understand. However, good analysts will have exponential smoothing techniques in their pocket to increase the value of their forecasts.
- Nature of Data: the nature of data useful for exponential smoothing is time series data . Time series data has time as part of its fields .
- Motive: the motive for exponential smoothing is to forecast future values with a smoothing variable.
Moving Average Technique
- Description: the moving average technique falls under the forecasting method and uses an average of recent values to predict future ones. For example, to predict rainfall in April, you would take the average of rainfall from January to March. It’s simple, yet highly effective.
- Importance: Very high. While I’m personally not a huge fan of moving averages due to their simplistic nature and lack of consideration for seasonality, they’re the most common forecasting technique and therefore very important.
- Nature of Data: the nature of data useful for moving averages is time series data .
- Motive: the motive for moving averages is to predict future values is a simple, easy-to-communicate way.
Neural Networks Technique
- Description: neural networks are a highly complex artificial intelligence technique that replicate a human’s neural analysis through a series of hyper-rapid computations and comparisons that evolve in real time. This technique is so complex that an analyst must use computer programs to perform it.
- Importance: Medium. While the potential for neural networks is theoretically unlimited, it’s still little understood and therefore uncommon. You do not need to know it by any means in order to be a data analyst.
- Nature of Data: the nature of data useful for neural networks is data sets of astronomical size, meaning with 100s of 1000s of fields and the same number of row at a minimum .
- Motive: the motive for neural networks is to understand wildly complex phenomenon and data to thereafter act on it.
Decision Tree Technique
- Description: the decision tree technique uses artificial intelligence algorithms to rapidly calculate possible decision pathways and their outcomes on a real-time basis. It’s so complex that computer programs are needed to perform it.
- Importance: Medium. As with neural networks, decision trees with AI are too little understood and are therefore uncommon in corporate and research settings alike.
- Nature of Data: the nature of data useful for the decision tree technique is hierarchical data sets that show multiple optional fields for each preceding field.
- Motive: the motive for decision tree techniques is to compute the optimal choices to make in order to achieve a desired result.
Evolutionary Programming Technique
- Description: the evolutionary programming technique uses a series of neural networks, sees how well each one fits a desired outcome, and selects only the best to test and retest. It’s called evolutionary because is resembles the process of natural selection by weeding out weaker options.
- Importance: Medium. As with the other AI techniques, evolutionary programming just isn’t well-understood enough to be usable in many cases. It’s complexity also makes it hard to explain in corporate settings and difficult to defend in research settings.
- Nature of Data: the nature of data in evolutionary programming is data sets of neural networks, or data sets of data sets.
- Motive: the motive for using evolutionary programming is similar to decision trees: understanding the best possible option from complex data.
- Video example :

Fuzzy Logic Technique
- Description: fuzzy logic is a type of computing based on “approximate truths” rather than simple truths such as “true” and “false.” It is essentially two tiers of classification. For example, to say whether “Apples are good,” you need to first classify that “Good is x, y, z.” Only then can you say apples are good. Another way to see it helping a computer see truth like humans do: “definitely true, probably true, maybe true, probably false, definitely false.”
- Importance: Medium. Like the other AI techniques, fuzzy logic is uncommon in both research and corporate settings, which means it’s less important in today’s world.
- Nature of Data: the nature of fuzzy logic data is huge data tables that include other huge data tables with a hierarchy including multiple subfields for each preceding field.
- Motive: the motive of fuzzy logic to replicate human truth valuations in a computer is to model human decisions based on past data. The obvious possible application is marketing.
Text Analysis Technique
- Description: text analysis techniques fall under the qualitative data analysis type and use text to extract insights.
- Importance: Medium. Text analysis techniques, like all the qualitative analysis type, are most valuable for researchers.
- Nature of Data: the nature of data useful in text analysis is words.
- Motive: the motive for text analysis is to trace themes in a text across sets of very long documents, such as books.
Coding Technique
- Description: the coding technique is used in textual analysis to turn ideas into uniform phrases and analyze the number of times and the ways in which those ideas appear. For this reason, some consider it a quantitative technique as well. You can learn more about coding and the other qualitative techniques here .
- Importance: Very high. If you’re a researcher working in social sciences, coding is THE analysis techniques, and for good reason. It’s a great way to add rigor to analysis. That said, it’s less common in corporate settings.
- Nature of Data: the nature of data useful for coding is long text documents.
- Motive: the motive for coding is to make tracing ideas on paper more than an exercise of the mind by quantifying it and understanding is through descriptive methods.
Idea Pattern Technique
- Description: the idea pattern analysis technique fits into coding as the second step of the process. Once themes and ideas are coded, simple descriptive analysis tests may be run. Some people even cluster the ideas!
- Importance: Very high. If you’re a researcher, idea pattern analysis is as important as the coding itself.
- Nature of Data: the nature of data useful for idea pattern analysis is already coded themes.
- Motive: the motive for the idea pattern technique is to trace ideas in otherwise unmanageably-large documents.
Word Frequency Technique
- Description: word frequency is a qualitative technique that stands in opposition to coding and uses an inductive approach to locate specific words in a document in order to understand its relevance. Word frequency is essentially the descriptive analysis of qualitative data because it uses stats like mean, median, and mode to gather insights.
- Importance: High. As with the other qualitative approaches, word frequency is very important in social science research, but less so in corporate settings.
- Nature of Data: the nature of data useful for word frequency is long, informative documents.
- Motive: the motive for word frequency is to locate target words to determine the relevance of a document in question.
Types of data analysis in research
Types of data analysis in research methodology include every item discussed in this article. As a list, they are:
- Quantitative
- Qualitative
- Mathematical
- Machine Learning and AI
- Descriptive
- Prescriptive
- Classification
- Forecasting
- Optimization
- Grounded theory
- Artificial Neural Networks
- Decision Trees
- Evolutionary Programming
- Fuzzy Logic
- Text analysis
- Idea Pattern Analysis
- Word Frequency Analysis
- Nïave Bayes
- Exponential smoothing
- Moving average
- Linear discriminant
Types of data analysis in qualitative research
As a list, the types of data analysis in qualitative research are the following methods:
Types of data analysis in quantitative research
As a list, the types of data analysis in quantitative research are:
Data analysis methods
As a list, data analysis methods are:
- Content (qualitative)
- Narrative (qualitative)
- Discourse (qualitative)
- Framework (qualitative)
- Grounded theory (qualitative)
Quantitative data analysis methods
As a list, quantitative data analysis methods are:
Tabular View of Data Analysis Types, Methods, and Techniques
| Types (Numeric or Non-numeric) | Quantitative |
| Qualitative | |
| Types tier 2 (Traditional Numeric or New Numeric) | Mathematical |
| Artificial Intelligence (AI) | |
| Types tier 3 (Informative Nature) | Descriptive |
| Diagnostic | |
| Predictive | |
| Prescriptive | |
| Methods | Clustering |
| Classification | |
| Forecasting | |
| Optimization | |
| Narrative analysis | |
| Discourse analysis | |
| Framework analysis | |
| Grounded theory | |
| Techniques | Clustering (doubles as technique) |
| Regression (linear and multivariable) | |
| Nïave Bayes | |
| Cohorts | |
| Factors | |
| Linear Discriminants | |
| Exponential smoothing | |
| Moving average | |
| Neural networks | |
| Decision trees | |
| Evolutionary programming | |
| Fuzzy logic | |
| Text analysis | |
| Coding | |
| Idea pattern analysis | |
| Word frequency |
About the Author
Noah is the founder & Editor-in-Chief at AnalystAnswers. He is a transatlantic professional and entrepreneur with 5+ years of corporate finance and data analytics experience, as well as 3+ years in consumer financial products and business software. He started AnalystAnswers to provide aspiring professionals with accessible explanations of otherwise dense finance and data concepts. Noah believes everyone can benefit from an analytical mindset in growing digital world. When he's not busy at work, Noah likes to explore new European cities, exercise, and spend time with friends and family.
File available immediately.

Notice: JavaScript is required for this content.
Have a language expert improve your writing
Run a free plagiarism check in 10 minutes, generate accurate citations for free.
- Knowledge Base
The Beginner's Guide to Statistical Analysis | 5 Steps & Examples
Statistical analysis means investigating trends, patterns, and relationships using quantitative data . It is an important research tool used by scientists, governments, businesses, and other organizations.
To draw valid conclusions, statistical analysis requires careful planning from the very start of the research process . You need to specify your hypotheses and make decisions about your research design, sample size, and sampling procedure.
After collecting data from your sample, you can organize and summarize the data using descriptive statistics . Then, you can use inferential statistics to formally test hypotheses and make estimates about the population. Finally, you can interpret and generalize your findings.
This article is a practical introduction to statistical analysis for students and researchers. We’ll walk you through the steps using two research examples. The first investigates a potential cause-and-effect relationship, while the second investigates a potential correlation between variables.
Table of contents
Step 1: write your hypotheses and plan your research design, step 2: collect data from a sample, step 3: summarize your data with descriptive statistics, step 4: test hypotheses or make estimates with inferential statistics, step 5: interpret your results, other interesting articles.
To collect valid data for statistical analysis, you first need to specify your hypotheses and plan out your research design.
Writing statistical hypotheses
The goal of research is often to investigate a relationship between variables within a population . You start with a prediction, and use statistical analysis to test that prediction.
A statistical hypothesis is a formal way of writing a prediction about a population. Every research prediction is rephrased into null and alternative hypotheses that can be tested using sample data.
While the null hypothesis always predicts no effect or no relationship between variables, the alternative hypothesis states your research prediction of an effect or relationship.
- Null hypothesis: A 5-minute meditation exercise will have no effect on math test scores in teenagers.
- Alternative hypothesis: A 5-minute meditation exercise will improve math test scores in teenagers.
- Null hypothesis: Parental income and GPA have no relationship with each other in college students.
- Alternative hypothesis: Parental income and GPA are positively correlated in college students.
Planning your research design
A research design is your overall strategy for data collection and analysis. It determines the statistical tests you can use to test your hypothesis later on.
First, decide whether your research will use a descriptive, correlational, or experimental design. Experiments directly influence variables, whereas descriptive and correlational studies only measure variables.
- In an experimental design , you can assess a cause-and-effect relationship (e.g., the effect of meditation on test scores) using statistical tests of comparison or regression.
- In a correlational design , you can explore relationships between variables (e.g., parental income and GPA) without any assumption of causality using correlation coefficients and significance tests.
- In a descriptive design , you can study the characteristics of a population or phenomenon (e.g., the prevalence of anxiety in U.S. college students) using statistical tests to draw inferences from sample data.
Your research design also concerns whether you’ll compare participants at the group level or individual level, or both.
- In a between-subjects design , you compare the group-level outcomes of participants who have been exposed to different treatments (e.g., those who performed a meditation exercise vs those who didn’t).
- In a within-subjects design , you compare repeated measures from participants who have participated in all treatments of a study (e.g., scores from before and after performing a meditation exercise).
- In a mixed (factorial) design , one variable is altered between subjects and another is altered within subjects (e.g., pretest and posttest scores from participants who either did or didn’t do a meditation exercise).
- Experimental
- Correlational
First, you’ll take baseline test scores from participants. Then, your participants will undergo a 5-minute meditation exercise. Finally, you’ll record participants’ scores from a second math test.
In this experiment, the independent variable is the 5-minute meditation exercise, and the dependent variable is the math test score from before and after the intervention. Example: Correlational research design In a correlational study, you test whether there is a relationship between parental income and GPA in graduating college students. To collect your data, you will ask participants to fill in a survey and self-report their parents’ incomes and their own GPA.
Measuring variables
When planning a research design, you should operationalize your variables and decide exactly how you will measure them.
For statistical analysis, it’s important to consider the level of measurement of your variables, which tells you what kind of data they contain:
- Categorical data represents groupings. These may be nominal (e.g., gender) or ordinal (e.g. level of language ability).
- Quantitative data represents amounts. These may be on an interval scale (e.g. test score) or a ratio scale (e.g. age).
Many variables can be measured at different levels of precision. For example, age data can be quantitative (8 years old) or categorical (young). If a variable is coded numerically (e.g., level of agreement from 1–5), it doesn’t automatically mean that it’s quantitative instead of categorical.
Identifying the measurement level is important for choosing appropriate statistics and hypothesis tests. For example, you can calculate a mean score with quantitative data, but not with categorical data.
In a research study, along with measures of your variables of interest, you’ll often collect data on relevant participant characteristics.
| Variable | Type of data |
|---|---|
| Age | Quantitative (ratio) |
| Gender | Categorical (nominal) |
| Race or ethnicity | Categorical (nominal) |
| Baseline test scores | Quantitative (interval) |
| Final test scores | Quantitative (interval) |
| Parental income | Quantitative (ratio) |
|---|---|
| GPA | Quantitative (interval) |
Prevent plagiarism. Run a free check.
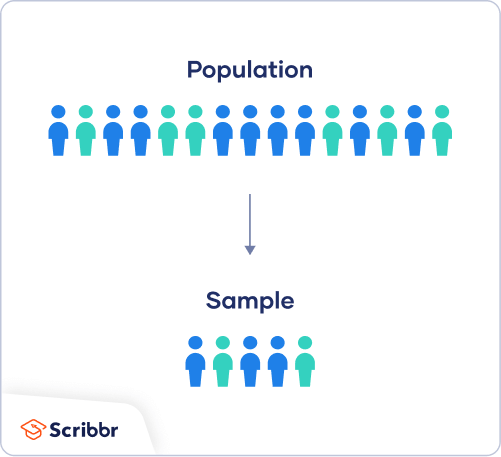
In most cases, it’s too difficult or expensive to collect data from every member of the population you’re interested in studying. Instead, you’ll collect data from a sample.
Statistical analysis allows you to apply your findings beyond your own sample as long as you use appropriate sampling procedures . You should aim for a sample that is representative of the population.
Sampling for statistical analysis
There are two main approaches to selecting a sample.
- Probability sampling: every member of the population has a chance of being selected for the study through random selection.
- Non-probability sampling: some members of the population are more likely than others to be selected for the study because of criteria such as convenience or voluntary self-selection.
In theory, for highly generalizable findings, you should use a probability sampling method. Random selection reduces several types of research bias , like sampling bias , and ensures that data from your sample is actually typical of the population. Parametric tests can be used to make strong statistical inferences when data are collected using probability sampling.
But in practice, it’s rarely possible to gather the ideal sample. While non-probability samples are more likely to at risk for biases like self-selection bias , they are much easier to recruit and collect data from. Non-parametric tests are more appropriate for non-probability samples, but they result in weaker inferences about the population.
If you want to use parametric tests for non-probability samples, you have to make the case that:
- your sample is representative of the population you’re generalizing your findings to.
- your sample lacks systematic bias.
Keep in mind that external validity means that you can only generalize your conclusions to others who share the characteristics of your sample. For instance, results from Western, Educated, Industrialized, Rich and Democratic samples (e.g., college students in the US) aren’t automatically applicable to all non-WEIRD populations.
If you apply parametric tests to data from non-probability samples, be sure to elaborate on the limitations of how far your results can be generalized in your discussion section .
Create an appropriate sampling procedure
Based on the resources available for your research, decide on how you’ll recruit participants.
- Will you have resources to advertise your study widely, including outside of your university setting?
- Will you have the means to recruit a diverse sample that represents a broad population?
- Do you have time to contact and follow up with members of hard-to-reach groups?
Your participants are self-selected by their schools. Although you’re using a non-probability sample, you aim for a diverse and representative sample. Example: Sampling (correlational study) Your main population of interest is male college students in the US. Using social media advertising, you recruit senior-year male college students from a smaller subpopulation: seven universities in the Boston area.
Calculate sufficient sample size
Before recruiting participants, decide on your sample size either by looking at other studies in your field or using statistics. A sample that’s too small may be unrepresentative of the sample, while a sample that’s too large will be more costly than necessary.
There are many sample size calculators online. Different formulas are used depending on whether you have subgroups or how rigorous your study should be (e.g., in clinical research). As a rule of thumb, a minimum of 30 units or more per subgroup is necessary.
To use these calculators, you have to understand and input these key components:
- Significance level (alpha): the risk of rejecting a true null hypothesis that you are willing to take, usually set at 5%.
- Statistical power : the probability of your study detecting an effect of a certain size if there is one, usually 80% or higher.
- Expected effect size : a standardized indication of how large the expected result of your study will be, usually based on other similar studies.
- Population standard deviation: an estimate of the population parameter based on a previous study or a pilot study of your own.
Once you’ve collected all of your data, you can inspect them and calculate descriptive statistics that summarize them.
Inspect your data
There are various ways to inspect your data, including the following:
- Organizing data from each variable in frequency distribution tables .
- Displaying data from a key variable in a bar chart to view the distribution of responses.
- Visualizing the relationship between two variables using a scatter plot .
By visualizing your data in tables and graphs, you can assess whether your data follow a skewed or normal distribution and whether there are any outliers or missing data.
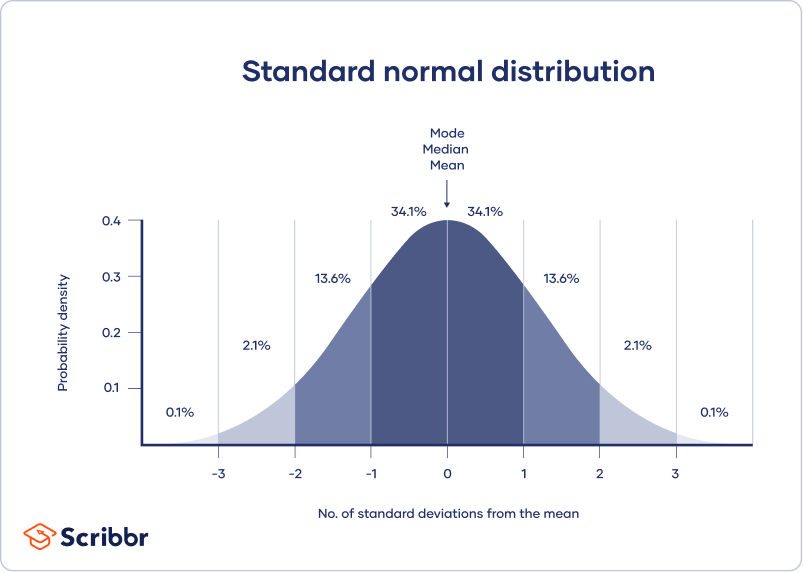
A normal distribution means that your data are symmetrically distributed around a center where most values lie, with the values tapering off at the tail ends.
In contrast, a skewed distribution is asymmetric and has more values on one end than the other. The shape of the distribution is important to keep in mind because only some descriptive statistics should be used with skewed distributions.
Extreme outliers can also produce misleading statistics, so you may need a systematic approach to dealing with these values.
Calculate measures of central tendency
Measures of central tendency describe where most of the values in a data set lie. Three main measures of central tendency are often reported:
- Mode : the most popular response or value in the data set.
- Median : the value in the exact middle of the data set when ordered from low to high.
- Mean : the sum of all values divided by the number of values.
However, depending on the shape of the distribution and level of measurement, only one or two of these measures may be appropriate. For example, many demographic characteristics can only be described using the mode or proportions, while a variable like reaction time may not have a mode at all.
Calculate measures of variability
Measures of variability tell you how spread out the values in a data set are. Four main measures of variability are often reported:
- Range : the highest value minus the lowest value of the data set.
- Interquartile range : the range of the middle half of the data set.
- Standard deviation : the average distance between each value in your data set and the mean.
- Variance : the square of the standard deviation.
Once again, the shape of the distribution and level of measurement should guide your choice of variability statistics. The interquartile range is the best measure for skewed distributions, while standard deviation and variance provide the best information for normal distributions.
Using your table, you should check whether the units of the descriptive statistics are comparable for pretest and posttest scores. For example, are the variance levels similar across the groups? Are there any extreme values? If there are, you may need to identify and remove extreme outliers in your data set or transform your data before performing a statistical test.
| Pretest scores | Posttest scores | |
|---|---|---|
| Mean | 68.44 | 75.25 |
| Standard deviation | 9.43 | 9.88 |
| Variance | 88.96 | 97.96 |
| Range | 36.25 | 45.12 |
| 30 | ||
From this table, we can see that the mean score increased after the meditation exercise, and the variances of the two scores are comparable. Next, we can perform a statistical test to find out if this improvement in test scores is statistically significant in the population. Example: Descriptive statistics (correlational study) After collecting data from 653 students, you tabulate descriptive statistics for annual parental income and GPA.
It’s important to check whether you have a broad range of data points. If you don’t, your data may be skewed towards some groups more than others (e.g., high academic achievers), and only limited inferences can be made about a relationship.
| Parental income (USD) | GPA | |
|---|---|---|
| Mean | 62,100 | 3.12 |
| Standard deviation | 15,000 | 0.45 |
| Variance | 225,000,000 | 0.16 |
| Range | 8,000–378,000 | 2.64–4.00 |
| 653 | ||
A number that describes a sample is called a statistic , while a number describing a population is called a parameter . Using inferential statistics , you can make conclusions about population parameters based on sample statistics.
Researchers often use two main methods (simultaneously) to make inferences in statistics.
- Estimation: calculating population parameters based on sample statistics.
- Hypothesis testing: a formal process for testing research predictions about the population using samples.
You can make two types of estimates of population parameters from sample statistics:
- A point estimate : a value that represents your best guess of the exact parameter.
- An interval estimate : a range of values that represent your best guess of where the parameter lies.
If your aim is to infer and report population characteristics from sample data, it’s best to use both point and interval estimates in your paper.
You can consider a sample statistic a point estimate for the population parameter when you have a representative sample (e.g., in a wide public opinion poll, the proportion of a sample that supports the current government is taken as the population proportion of government supporters).
There’s always error involved in estimation, so you should also provide a confidence interval as an interval estimate to show the variability around a point estimate.
A confidence interval uses the standard error and the z score from the standard normal distribution to convey where you’d generally expect to find the population parameter most of the time.
Hypothesis testing
Using data from a sample, you can test hypotheses about relationships between variables in the population. Hypothesis testing starts with the assumption that the null hypothesis is true in the population, and you use statistical tests to assess whether the null hypothesis can be rejected or not.
Statistical tests determine where your sample data would lie on an expected distribution of sample data if the null hypothesis were true. These tests give two main outputs:
- A test statistic tells you how much your data differs from the null hypothesis of the test.
- A p value tells you the likelihood of obtaining your results if the null hypothesis is actually true in the population.
Statistical tests come in three main varieties:
- Comparison tests assess group differences in outcomes.
- Regression tests assess cause-and-effect relationships between variables.
- Correlation tests assess relationships between variables without assuming causation.
Your choice of statistical test depends on your research questions, research design, sampling method, and data characteristics.
Parametric tests
Parametric tests make powerful inferences about the population based on sample data. But to use them, some assumptions must be met, and only some types of variables can be used. If your data violate these assumptions, you can perform appropriate data transformations or use alternative non-parametric tests instead.
A regression models the extent to which changes in a predictor variable results in changes in outcome variable(s).
- A simple linear regression includes one predictor variable and one outcome variable.
- A multiple linear regression includes two or more predictor variables and one outcome variable.
Comparison tests usually compare the means of groups. These may be the means of different groups within a sample (e.g., a treatment and control group), the means of one sample group taken at different times (e.g., pretest and posttest scores), or a sample mean and a population mean.
- A t test is for exactly 1 or 2 groups when the sample is small (30 or less).
- A z test is for exactly 1 or 2 groups when the sample is large.
- An ANOVA is for 3 or more groups.
The z and t tests have subtypes based on the number and types of samples and the hypotheses:
- If you have only one sample that you want to compare to a population mean, use a one-sample test .
- If you have paired measurements (within-subjects design), use a dependent (paired) samples test .
- If you have completely separate measurements from two unmatched groups (between-subjects design), use an independent (unpaired) samples test .
- If you expect a difference between groups in a specific direction, use a one-tailed test .
- If you don’t have any expectations for the direction of a difference between groups, use a two-tailed test .
The only parametric correlation test is Pearson’s r . The correlation coefficient ( r ) tells you the strength of a linear relationship between two quantitative variables.
However, to test whether the correlation in the sample is strong enough to be important in the population, you also need to perform a significance test of the correlation coefficient, usually a t test, to obtain a p value. This test uses your sample size to calculate how much the correlation coefficient differs from zero in the population.
You use a dependent-samples, one-tailed t test to assess whether the meditation exercise significantly improved math test scores. The test gives you:
- a t value (test statistic) of 3.00
- a p value of 0.0028
Although Pearson’s r is a test statistic, it doesn’t tell you anything about how significant the correlation is in the population. You also need to test whether this sample correlation coefficient is large enough to demonstrate a correlation in the population.
A t test can also determine how significantly a correlation coefficient differs from zero based on sample size. Since you expect a positive correlation between parental income and GPA, you use a one-sample, one-tailed t test. The t test gives you:
- a t value of 3.08
- a p value of 0.001
Receive feedback on language, structure, and formatting
Professional editors proofread and edit your paper by focusing on:
- Academic style
- Vague sentences
- Style consistency
See an example
The final step of statistical analysis is interpreting your results.
Statistical significance
In hypothesis testing, statistical significance is the main criterion for forming conclusions. You compare your p value to a set significance level (usually 0.05) to decide whether your results are statistically significant or non-significant.
Statistically significant results are considered unlikely to have arisen solely due to chance. There is only a very low chance of such a result occurring if the null hypothesis is true in the population.
This means that you believe the meditation intervention, rather than random factors, directly caused the increase in test scores. Example: Interpret your results (correlational study) You compare your p value of 0.001 to your significance threshold of 0.05. With a p value under this threshold, you can reject the null hypothesis. This indicates a statistically significant correlation between parental income and GPA in male college students.
Note that correlation doesn’t always mean causation, because there are often many underlying factors contributing to a complex variable like GPA. Even if one variable is related to another, this may be because of a third variable influencing both of them, or indirect links between the two variables.
Effect size
A statistically significant result doesn’t necessarily mean that there are important real life applications or clinical outcomes for a finding.
In contrast, the effect size indicates the practical significance of your results. It’s important to report effect sizes along with your inferential statistics for a complete picture of your results. You should also report interval estimates of effect sizes if you’re writing an APA style paper .
With a Cohen’s d of 0.72, there’s medium to high practical significance to your finding that the meditation exercise improved test scores. Example: Effect size (correlational study) To determine the effect size of the correlation coefficient, you compare your Pearson’s r value to Cohen’s effect size criteria.
Decision errors
Type I and Type II errors are mistakes made in research conclusions. A Type I error means rejecting the null hypothesis when it’s actually true, while a Type II error means failing to reject the null hypothesis when it’s false.
You can aim to minimize the risk of these errors by selecting an optimal significance level and ensuring high power . However, there’s a trade-off between the two errors, so a fine balance is necessary.
Frequentist versus Bayesian statistics
Traditionally, frequentist statistics emphasizes null hypothesis significance testing and always starts with the assumption of a true null hypothesis.
However, Bayesian statistics has grown in popularity as an alternative approach in the last few decades. In this approach, you use previous research to continually update your hypotheses based on your expectations and observations.
Bayes factor compares the relative strength of evidence for the null versus the alternative hypothesis rather than making a conclusion about rejecting the null hypothesis or not.
If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.
- Student’s t -distribution
- Normal distribution
- Null and Alternative Hypotheses
- Chi square tests
- Confidence interval
Methodology
- Cluster sampling
- Stratified sampling
- Data cleansing
- Reproducibility vs Replicability
- Peer review
- Likert scale
Research bias
- Implicit bias
- Framing effect
- Cognitive bias
- Placebo effect
- Hawthorne effect
- Hostile attribution bias
- Affect heuristic
Is this article helpful?
Other students also liked.
- Descriptive Statistics | Definitions, Types, Examples
- Inferential Statistics | An Easy Introduction & Examples
- Choosing the Right Statistical Test | Types & Examples
More interesting articles
- Akaike Information Criterion | When & How to Use It (Example)
- An Easy Introduction to Statistical Significance (With Examples)
- An Introduction to t Tests | Definitions, Formula and Examples
- ANOVA in R | A Complete Step-by-Step Guide with Examples
- Central Limit Theorem | Formula, Definition & Examples
- Central Tendency | Understanding the Mean, Median & Mode
- Chi-Square (Χ²) Distributions | Definition & Examples
- Chi-Square (Χ²) Table | Examples & Downloadable Table
- Chi-Square (Χ²) Tests | Types, Formula & Examples
- Chi-Square Goodness of Fit Test | Formula, Guide & Examples
- Chi-Square Test of Independence | Formula, Guide & Examples
- Coefficient of Determination (R²) | Calculation & Interpretation
- Correlation Coefficient | Types, Formulas & Examples
- Frequency Distribution | Tables, Types & Examples
- How to Calculate Standard Deviation (Guide) | Calculator & Examples
- How to Calculate Variance | Calculator, Analysis & Examples
- How to Find Degrees of Freedom | Definition & Formula
- How to Find Interquartile Range (IQR) | Calculator & Examples
- How to Find Outliers | 4 Ways with Examples & Explanation
- How to Find the Geometric Mean | Calculator & Formula
- How to Find the Mean | Definition, Examples & Calculator
- How to Find the Median | Definition, Examples & Calculator
- How to Find the Mode | Definition, Examples & Calculator
- How to Find the Range of a Data Set | Calculator & Formula
- Hypothesis Testing | A Step-by-Step Guide with Easy Examples
- Interval Data and How to Analyze It | Definitions & Examples
- Levels of Measurement | Nominal, Ordinal, Interval and Ratio
- Linear Regression in R | A Step-by-Step Guide & Examples
- Missing Data | Types, Explanation, & Imputation
- Multiple Linear Regression | A Quick Guide (Examples)
- Nominal Data | Definition, Examples, Data Collection & Analysis
- Normal Distribution | Examples, Formulas, & Uses
- Null and Alternative Hypotheses | Definitions & Examples
- One-way ANOVA | When and How to Use It (With Examples)
- Ordinal Data | Definition, Examples, Data Collection & Analysis
- Parameter vs Statistic | Definitions, Differences & Examples
- Pearson Correlation Coefficient (r) | Guide & Examples
- Poisson Distributions | Definition, Formula & Examples
- Probability Distribution | Formula, Types, & Examples
- Quartiles & Quantiles | Calculation, Definition & Interpretation
- Ratio Scales | Definition, Examples, & Data Analysis
- Simple Linear Regression | An Easy Introduction & Examples
- Skewness | Definition, Examples & Formula
- Statistical Power and Why It Matters | A Simple Introduction
- Student's t Table (Free Download) | Guide & Examples
- T-distribution: What it is and how to use it
- Test statistics | Definition, Interpretation, and Examples
- The Standard Normal Distribution | Calculator, Examples & Uses
- Two-Way ANOVA | Examples & When To Use It
- Type I & Type II Errors | Differences, Examples, Visualizations
- Understanding Confidence Intervals | Easy Examples & Formulas
- Understanding P values | Definition and Examples
- Variability | Calculating Range, IQR, Variance, Standard Deviation
- What is Effect Size and Why Does It Matter? (Examples)
- What Is Kurtosis? | Definition, Examples & Formula
- What Is Standard Error? | How to Calculate (Guide with Examples)
What is your plagiarism score?

IMAGES
VIDEO