mathematical modeling essay

Loading metrics

Open Access

Ten simple rules for tackling your first mathematical models: A guide for graduate students by graduate students

Roles Conceptualization, Investigation, Writing – original draft, Writing – review & editing

* E-mail: [email protected]

Affiliations Department of Biological Sciences, University of Toronto Scarborough, Toronto, Ontario, Canada, Department of Ecology and Evolution, University of Toronto, Toronto, Ontario, Canada

Affiliation Department of Ecology and Evolution, University of Toronto, Toronto, Ontario, Canada

Affiliation Department of Physical and Environmental Sciences, University of Toronto Scarborough, Toronto, Ontario, Canada

Affiliation Department of Biology, Memorial University of Newfoundland, St John’s, Newfoundland, Canada

• Korryn Bodner, 
• Chris Brimacombe, 
• Emily S. Chenery, 
• Ariel Greiner, 
• Anne M. McLeod, 
• Stephanie R. Penk, 
• Juan S. Vargas Soto

Published: January 14, 2021

• https://doi.org/10.1371/journal.pcbi.1008539
• Reader Comments

Citation: Bodner K, Brimacombe C, Chenery ES, Greiner A, McLeod AM, Penk SR, et al. (2021) Ten simple rules for tackling your first mathematical models: A guide for graduate students by graduate students. PLoS Comput Biol 17(1): e1008539. https://doi.org/10.1371/journal.pcbi.1008539

Editor: Scott Markel, Dassault Systemes BIOVIA, UNITED STATES

Copyright: © 2021 Bodner et al. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

Funding: The authors received no specific funding for this work.

Competing interests: The authors have declared that no competing interests exist.

Introduction

Biologists spend their time studying the natural world, seeking to understand its various patterns and the processes that give rise to them. One way of furthering our understanding of natural phenomena is through laboratory or field experiments, examining the effects of changing one, or several, variables on a measured response. Alternatively, one may conduct an observational study, collecting field data and comparing a measured response along natural gradients. A third and complementary way of understanding natural phenomena is through mathematical models. In the life sciences, more scientists are incorporating these quantitative methods into their research. Given the vast utility of mathematical models, ranging from providing qualitative predictions to helping disentangle multiple causation (see Hurford [ 1 ] for a more complete list), their increased adoption is unsurprising. However, getting started with mathematical models may be quite daunting for those with traditional biological training, as in addition to understanding new terminology (e.g., “Jacobian matrix,” “Markov chain”), one may also have to adopt a different way of thinking and master a new set of skills.

Here, we present 10 simple rules for tackling your first mathematical models. While many of these rules are applicable to basic scientific research, our discussion relates explicitly to the process of model-building within ecological and epidemiological contexts using dynamical models. However, many of the suggestions outlined below generalize beyond these disciplines and are applicable to nondynamic models such as statistical models and machine-learning algorithms. As graduate students ourselves, we have created rules we wish we had internalized before beginning our model-building journey—a guide by graduate students, for graduate students—and we hope they prove insightful for anyone seeking to begin their own adventures in mathematical modelling.

• PPT PowerPoint slide
• PNG larger image
• TIFF original image

Boxes represent susceptible, infected, and recovered compartments, and directed arrows represent the flow of individuals between these compartments with the rate of flow being controlled by the contact rate, c , the probability of infection, γ , and the recovery rate, θ .

https://doi.org/10.1371/journal.pcbi.1008539.g001

Rule 1: Know your question

“All models are wrong, some are useful” is a common aphorism, generally attributed to statistician George Box, but determining which models are useful is dependent upon the question being asked. The practice of clearly defining a research question is often drilled into aspiring researchers in the context of selecting an appropriate research design, interpreting statistical results, or when outlining a research paper. Similarly, the practice of defining a clear research question is important for mathematical models as their results are only as interesting as the questions that motivate them [ 5 ]. The question defines the model’s main purpose and, in all cases, should extend past the goal of merely building a model for a system (the question can even answer whether a model is even necessary). Ultimately, the model should provide an answer to the research question that has been proposed.

When the research question is used to inform the purpose of the model, it also informs the model’s structure. Given that models can be modified in countless ways, providing a purpose to the model can highlight why certain aspects of reality were included in the structure while others were ignored [ 6 ]. For example, when deciding whether we should adopt a more realistic model (i.e., add more complexity), we can ask whether we are trying to inform general theory or whether we are trying to model a response in a specific system. For example, perhaps we are trying to predict how fast an epidemic will grow based on different age-dependent mixing patterns. In this case, we may wish to adapt our basic SIR model to have age-structured compartments if we suspect this factor is important for the disease dynamics. However, if we are exploring a different question, such as how stochasticity influences general SIR dynamics, the age-structured approach would likely be unnecessary. We suggest that one of the first steps in any modelling journey is to choose the processes most relevant to your question (i.e., your hypothesis) and the direct and indirect causal relationships among them: Are the relationships linear, nonlinear, additive, or multiplicative? This challenge can be aided with a good literature review. Depending on your model purpose, you may also need to spend extra time getting to know your system and/or the data before progressing forward. Indeed, the more background knowledge acquired when forming your research question, the more informed your decision-making when selecting the structure, parameters, and data for your model.

Rule 2: Define multiple appropriate models

Natural phenomena are complicated to study and often impossible to model in their entirety. We are often unsure about the variables or processes required to fully answer our research question(s). For example, we may not know how the possibility of reinfection influences the dynamics of a disease system. In cases such as these, our advice is to produce and sketch out a set of candidate models that consider alternative terms/variables which may be relevant for the phenomena under investigation. As in Fig 2 , we construct 2 models, one that includes the ability for recovered individuals to become infected again, and one that does not. When creating multiple models, our general objective may be to explore how different processes, inputs, or drivers affect an outcome of interest or it may be to find a model or models that best explain a given set of data for an outcome of interest. In our example, if the objective is to determine whether reinfection plays an important role in explaining the patterns of a disease, we can test our SIR candidate models using incidence data to determine which model receives the most empirical support. Here we consider our candidate models to be alternative hypotheses, where the candidate model with the least support is discarded. While our perspective of models as hypotheses is a view shared by researchers such as Hilborn and Mangel [ 7 ], and Penk and colleagues [ 8 ], please note that others such as Oreskes and colleagues [ 9 ] believe that models are not subject to proof and hence disagree with this notion. We encourage modellers who are interested in this debate to read the provided citations.

(A) A susceptible/infected/recovered model where individuals remain immune (gold) and (B) a susceptible/infected/recovered model where individuals can become susceptible again (blue). Arrows indicate the direction of movement between compartments, c is the contact rate, γ is the infection rate given contact, and θ is the recovery rate. The text below each conceptual model are the hypotheses ( H1 and H2 ) that represent the differences between these 2 SIR models.

https://doi.org/10.1371/journal.pcbi.1008539.g002

Finally, we recognize that time and resource constraints may limit the ability to build multiple models simultaneously; however, even writing down alternative models on paper can be helpful as you can always revisit them if your primary model does not perform as expected. Of course, some candidate models may not be feasible or relevant for your system, but by engaging in the activity of creating multiple models, you will likely have a broader perspective of the potential factors and processes that fundamentally shape your system.

Rule 3: Determine the skills you will need (and how to get them)

Equipping yourself with the necessary analytical tools that form the basis of all quantitative techniques is essential. As Darwin said, those that have knowledge of mathematics seem to be endowed with an extra sense [ 10 ], and having a background in calculus, linear algebra, and statistics can go a long way. Thus, make it a habit to set time for yourself to learn these mathematical skills, and do not treat all your methods like a black box. For instance, if you plan to use ODEs, consider brushing up on your calculus, e.g., using Stewart [ 11 ]. If you are working with a system of ODEs, also read up on linear algebra, e.g., using Poole [ 12 ]. Some universities also offer specialized math biology courses that combine topics from different math courses to teach the essentials of mathematical modelling. Taking these courses can help save time, and if they are not available, their syllabi can help focus your studying. Also note that while narrowing down a useful skillset in the early stages of model-building will likely spare you from some future headaches, as you progress in your project, it is inevitable that new skills will be required. Therefore, we advise you to check in at different stages of your modelling journey to assess the skills that would be most relevant for your next steps and how best to acquire them. Hopefully, these decisions can also be made with the help of your supervisor and/or a modelling mentor. Building these extra skills can at first seem daunting but think of it as an investment that will pay dividends in improving your future modelling work.

When first attempting to tackle a specific problem, find relevant research that accomplishes the same tasks and determine if you understand the processes and techniques that are used in that study. If you do, then you can implement similar techniques and methods, and perhaps introduce new methods. If not, then determine which tools you need to add to your toolbox. For instance, if the problem involves a system of ODEs (e.g., SIR models, see above), can you use existing symbolic software (e.g., Maple, Matlab, Mathematica) to determine the systems dynamics via a general solution, or is the complexity too great that you will need to create simulations to infer the dynamics? Figuring out questions like these is key to understanding what skills you will need to work with the model you develop. While there is a time and a place for involving collaborators to help facilitate methods that are beyond your current reach, we strongly advocate that you approach any potential collaborator only after you have gained some knowledge of the methods first. Understanding the methodology, or at least its foundation, is not only crucial for making a fruitful collaboration, but also important for your development as a scientist.

Rule 4: Do not reinvent the wheel

While we encourage a thorough understanding of the methods researchers employ, we simultaneously discourage unnecessary effort redoing work that has already been done. Preventing duplication can be ensured by a thorough review of the literature (but note that reproducing original model results can advance your knowledge of how a model functions and lead to new insights in the system). Often, we are working from established theory that provides an existing framework that can be applied to different systems. Adapting these frameworks can help advance your own research while also saving precious time. When digging through articles, bear in mind that most modelling frameworks are not system-specific. Do not be discouraged if you cannot immediately find a model in your field, as the perfect model for your question may have been applied in a different system or be published only as a conceptual model. These models are still useful! Also, do not be shy about reaching out to authors of models that you think may be applicable to your system. Finally, remember that you can be critical of what you find, as some models can be deceptively simple or involve assumptions that you are not comfortable making. You should not reinvent the wheel, but you can always strive to build a better one.

Rule 5: Study and apply good coding practices

The modelling process will inevitably require some degree of programming, and this can quickly become a challenge for some biologists. However, learning to program in languages commonly adopted by the scientific community (e.g., R, Python) can increase the transparency, accessibility, and reproducibility of your models. Even if you only wish to adopt preprogrammed models, you will likely still need to create code of your own that reads in data, applies functions from a collection of packages to analyze the data, and creates some visual output. Programming can be highly rewarding—you are creating something after all—but it can also be one of the most frustrating parts of your research. What follows are 3 suggestions to avoid some of the frustration.

Organization is key, both in your workflow and your written code. Take advantage of existing software and tools that facilitate keeping things organized. For example, computational notebooks like Jupyter notebooks or R-Markdown documents allow you to combine text, commands, and outputs in an easily readable and shareable format. Version control software like Git makes it simple to both keep track of changes as well as to safely explore different model variants via branches without worrying that the original model has been altered. Additionally, integrating with hosting services such as Github allows you to keep your changes safely stored in the cloud. For more details on learning to program, creating reproducible research, programming with Jupyter notebooks, and using Git and Github, see the 10 simple rules by Carey and Papin [ 13 ], Sandve and colleagues [ 14 ], Rule and colleagues [ 15 ], and Perez-Riverol and colleagues [ 16 ], respectively.

Comment your code and comment it well (see Fig 3 ). These comments can be the pseudocode you have written on paper prior to coding. Assume that when you revisit your code weeks, months, or years later, you will have forgotten most of what you did and why you did it. Good commenting can also help others read and use your code, making it a critical part of increasing scientific transparency. It is always good practice to write your comments before you write the code, explaining what the code should do. When coding a function, include a description of its inputs and outputs. We also encourage you to publish your commented model code in repositories such that they are easily accessible to others—not only to get useful feedback for yourself but to provide the modelling foundation for others to build on.

Two functionally identical codes in R [ 17 ] can look very different without comments (left) and with descriptive comments (right). Writing detailed comments will help you and others understand, adapt, and use your code.

https://doi.org/10.1371/journal.pcbi.1008539.g003

When writing long code, test portions of it separately. If you are writing code that will require a lot of processing power or memory to run, use a simple example first, both to estimate how long the project will take, and to avoid waiting 12 hours to see if it works. Additionally, when writing code, try to avoid too many packages and “tricks” as it can make your code more difficult to understand. Do not be afraid of writing 2 separate functions if it will make your code more intuitive. As with writing, your skill as a writer is not dependent on your ability to use big words, but instead about making sure your reader understands what you are trying to communicate.

Rule 6: Sweat the “right” small stuff

By “sweat the ‘right’ small stuff,” we mean considering the details and assumptions that can potentially make or break a mathematical model. A good start would be to ensure your model follows the rules of mass and energy conservation. In a closed system, mass and energy cannot be created nor destroyed, and thus, the left side of the mathematical equation must equal the right under all circumstances. For example, in Eq 2 , if the number of susceptible individuals decreases due to infection, we must include a negative term in this equation (− cγIS ) to indicate that loss and its conjugate (+ cγIS ) to the infected individuals equation, Eq 3 , to represent that gain. Similarly, units of all terms must also be balanced on both sides of the equation. For example, if we wish to add or subtract 2 values, we must ensure their units are equivalent (e.g., cannot add day −1 and year −1 ). Simple oversights in units can lead to major setbacks and create bizarre dynamics, so it is worth taking the time to ensure the units match up.

Modellers should also consider the fundamental boundary conditions of each parameter to determine if there are some values that are illogical. Logical constraints and boundaries can be developed for each parameter using prior knowledge and assumptions (e.g., Huntley [ 18 ]). For example, when considering an SIR model, there are 2 parameters that comprise the transmission rate—the contact rate, c , and the probability of infection given contact, γ . Using our intuition, we can establish some basic rules: (1) the contact rate cannot be negative; (2) the number of susceptible, infected, and recovered individuals cannot be below 0; and (3) the probability of infection given contact must fall between 0 and 1. Keeping these in mind as you test your model’s dynamics can alert you to problems in your model’s structure. Finally, simulating your model is an excellent method to obtain more reasonable bounds for inputs and parameters and ensure behavior is as expected. See Otto and Day [ 5 ] for more information on the “basic ingredients” of model-building.

Rule 7: Simulate, simulate, simulate

Even though there is a lot to be learned from analyzing simple models and their general solutions, modelling a complex world sometimes requires complex equations. Unfortunately, the cost of this complexity is often the loss of general solutions [ 19 ]. Instead, many biologists must calculate a numerical solution, an approximate solution, and simulate the dynamics of these models [ 20 ]. Simulations allow us to explore model behavior, given different structures, initial conditions, and parameters ( Fig 4 ). Importantly, they allow us to understand the dynamics of complex systems that may otherwise not be ethical, feasible, or economically viable to explore in natural systems [ 21 ].

Gold lines represent the SIR structure ( Fig 2A ) where lifelong immunity of individuals is inferred after infection, and blue lines represent an SIRS structure ( Fig 2B ) where immunity is lost over time. The solid lines represent model dynamics assuming a recovery rate ( θ ) of 0.05, while dotted lines represent dynamics assuming a recovery rate of 0.1. All model runs assume a transmission rate, cγ , of 0.2 and an immunity loss rate, ψ , of 0.01. By using simulations, we can explore how different processes and rates change the system’s dynamics and furthermore determine at what point in time these differences are detectable. SIR, Susceptible-Infected-Recovered; SIRS, Susceptible-Infected-Recovered-Susceptible.

https://doi.org/10.1371/journal.pcbi.1008539.g004

One common method of exploring the dynamics of complex systems is through sensitivity analysis (SA). We can use this simulation-based technique to ascertain how changes in parameters and initial conditions will influence the behavior of a system. For example, if simulated model outputs remain relatively similar despite large changes in a parameter value, we can expect the natural system represented by that model to be robust to similar perturbations. If instead, simulations are very sensitive to parameter values, we can expect the natural system to be sensitive to its variation. Here in Fig 4 , we can see that both SIR models are very sensitive to the recovery rate parameter ( θ ) suggesting that the natural system would also be sensitive to individuals’ recovery rates. We can therefore use SA to help inform which parameters are most important and to determine which are distinguishable (i.e., identifiable). Additionally, if observed system data are available, we can use SA to help us establish what are the reasonable boundaries for our initial conditions and parameters. When adopting SA, we can either vary parameters or initial conditions one at a time (local sensitivity) or preferably, vary multiple of them in tandem (global sensitivity). We recognize this topic may be overwhelming to those new to modelling so we recommend reading Marino and colleagues [ 22 ] and Saltelli and colleagues [ 23 ] for details on implementing different SA methods.

Simulations are also a useful tool for testing how accurately different model fitting approaches (e.g., Maximum Likelihood Estimation versus Bayesian Estimation) can recover parameters. Given that we know the parameter values for simulated model outputs (i.e., simulated data), we can properly evaluate the fitting procedures of methods when used on that simulated data. If your fitting approach cannot even recover simulated data with known parameters, it is highly unlikely your procedure will be successful given real, noisy data. If a procedure performs well under these conditions, try refitting your model to simulated data that more closely resembles your own dataset (i.e., imperfect data). If you know that there was limited sampling and/or imprecise tools used to collect your data, consider adding noise, reducing sample sizes, and adding temporal and spatial gaps to see if the fitting procedure continues to return reasonably correct estimates. Remember, even if your fitting procedures continue to perform well given these additional complexities, issues may still arise when fitting to empirical data. Models are approximations and consequently their simulations are imperfect representations of your measured outcome of interest. However, by evaluating procedures on perfectly known imperfect data, we are one step closer to having a fitting procedure that works for us even when it seems like our data are against us.

Rule 8: Expect model fitting to be a lengthy, arduous but creative task

Model fitting requires an understanding of both the assumptions and limitations of your model, as well as the specifics of the data to be used in the fitting. The latter can be challenging, particularly if you did not collect the data yourself, as there may be additional uncertainties regarding the sampling procedure, or the variables being measured. For example, the incidence data commonly adopted to fit SIR models often contain biases related to underreporting, selective reporting, and reporting delays [ 24 ]. Taking the time to understand the nuances of the data is critical to prevent mismatches between the model and the data. In a bad case, a mismatch may lead to a poor-fitting model. In the worst case, a model may appear well-fit, but will lead to incorrect inferences and predictions.

Model fitting, like all aspects of modelling, is easier with the appropriate set of skills (see Rule 2). In particular, being proficient at constructing and analyzing mathematical models does not mean you are prepared to fit them. Fitting models typically requires additional in-depth statistical knowledge related to the characteristics of probability distributions, deriving statistical moments, and selecting appropriate optimization procedures. Luckily, a substantial portion of this knowledge can be gleaned from textbooks and methods-based research articles. These resources can range from covering basic model fitting, such as determining an appropriate distribution for your data and constructing a likelihood for that distribution (e.g., Hilborn and Mangel [ 7 ]), to more advanced topics, such as accounting for uncertainties in parameters, inputs, and structures during model fitting (e.g., Dietze [ 25 ]). We find these sources among others (e.g., Hobbs and Hooten [ 26 ] for Bayesian methods; e.g., Adams and colleagues [ 27 ] for fitting noisy and sparse datasets; e.g., Sirén and colleagues [ 28 ] for fitting individual-based models; and Williams and Kendall [ 29 ] for multiobject optimization—to name a few) are not only useful when starting to fit your first models, but are also useful when switching from one technique or model to another.

After you have learned about your data and brushed up on your statistical knowledge, you may still run into issues when model fitting. If you are like us, you will have incomplete data, small sample sizes, and strange data idiosyncrasies that do not seem to be replicated anywhere else. At this point, we suggest you be explorative in the resources you use and accept that you may have to combine multiple techniques and/or data sources before it is feasible to achieve an adequate model fit (see Rosenbaum and colleagues [ 30 ] for parameter estimation with multiple datasets). Evaluating the strength of different techniques can be aided by using simulated data to test these techniques, while SA can be used to identify insensitive parameters which can often be ignored in the fitting process (see Rule 7).

Model accuracy is an important metric but “good” models are also precise (i.e., reliable). During model fitting, to make models more reliable, the uncertainties in their inputs, drivers, parameters, and structures, arising due to natural variability (i.e., aleatory uncertainty) or imperfect knowledge (i.e., epistemic uncertainty), should be identified, accounted for, and reduced where feasible [ 31 ]. Accounting for uncertainty may entail measurements of uncertainties being propagated through a model (a simple example being a confidence interval), while reducing uncertainty may require building new models or acquiring additional data that minimize the prioritized uncertainties (see Dietze [ 25 ] and Tsigkinopoulou and colleagues [ 32 ] for a more thorough review on the topic). Just remember that although the steps outlined in this rule may take a while to complete, when you do achieve a well-fitted reliable model, it is truly something to be celebrated.

Rule 9: Give yourself time (and then add more)

Experienced modellers know that it often takes considerable time to build a model and that even more time may be required when fitting to real data. However, the pervasive caricature of modelling as being “a few lines of code here and there” or “a couple of equations” can lead graduate students to hold unrealistic expectations of how long finishing a model may take (or when to consider a model “finished”). Given the multiple considerations that go into selecting and implementing models (see previous rules), it should be unsurprising that the modelling process may take weeks, months, or even years. Remembering that a published model is the final product of long and hard work may help reduce some of your time-based anxieties. In reality, the finished product is just the tip of the iceberg and often unseen is the set of failed or alternative models providing its foundation. Note that taking time early on to establish what is “good enough” given your objective, and to instill good modelling practices, such as developing multiple models, simulating your models, and creating well-documented code, can save you considerable time and stress.

Rule 10: Care about the process, not just the endpoint

As a graduate student, hours of labor coupled with relative inexperience may lead to an unwillingness to change to a new model later down the line. But being married to one model can restrict its efficacy, or worse, lead to incorrect conclusions. Early planning may mitigate some modelling problems, but many issues will only become apparent as time goes on. For example, perhaps model parameters cannot be estimated as you previously thought, or assumptions made during model formulation have since proven false. Modelling is a dynamic process, and some steps will need to be revisited many times as you correct, refine, and improve your model. It is also important to bear in mind that the process of model-building is worth the effort. The process of translating biological dynamics into mathematical equations typically forces us to question our assumptions, while a misspecified model often leads to novel insights. While we may wish we had the option to skip to a final finished product, in the words of Drake, “sometimes it’s the journey that teaches you a lot about your destination”.

There is no such thing as a failed model. With every new error message or wonky output, we learn something useful about modelling (mostly begrudgingly) and, if we are lucky, perhaps also about the study system. It is easy to cave in to the ever-present pressure to perform, but as graduate students, we are still learning. Luckily, you are likely surrounded by other graduate students, often facing similar challenges who can be an invaluable resource for learning and support. Finally, remember that it does not matter if this was your first or your 100th mathematical model, challenges will always present themselves. However, with practice and determination, you will become more skilled at overcoming them, allowing you to grow and take on even greater challenges.

Acknowledgments

We thank Marie-Josée Fortin, Martin Krkošek, Péter K. Molnár, Shawn Leroux, Carina Rauen Firkowski, Cole Brookson, Gracie F.Z. Wild, Cedric B. Hunter, and Philip E. Bourne for their helpful input on the manuscript.

• 1. Hurford A. Overview of mathematical modelling in biology II. 2012 [cite 2020 October 25]. Available: https://theartofmodelling.wordpress.com/2012/01/04/overview-of-mathematical-modelling-in-biology-ii/
• View Article
• PubMed/NCBI
• Google Scholar
• 3. Maki Y, Hirose H, ADSIR M. Infectious Disease Spread Analysis Using Stochastic Differential Equations for SIR Model. International Conference on Intelligent Systems, Modelling and Simulation. IEEE. 2013.
• 5. Otto SP, Day T. A biologist’s guide to mathematical modeling in ecology and evolution. Princeton, NJ: Princeton University Press; 2007.
• 7. Hilborn R, Mangel M. The ecological detective: Confronting models with data. Princeton, NJ: Princeton University Press; 1997.
• 10. Darwin C. The autobiography of Charles Darwin. Darwin F, editor. 2008. Available: https://www.gutenberg.org/files/2010/2010-h/2010-h.htm
• 11. Stewart J. Calculus: Early transcendentals. Eighth. Boston, MA: Cengage Learning; 2015.
• 12. Poole D. Linear algebra: A modern introduction. Fourth. Stamford, CT: Cengage Learning; 2014.
• 17. R Core Team. R: A language and environment for statistical computing (version 3.6.0, R foundation for statistical computing). 2020.
• 18. Huntley HE. Dimensional analysis. First. New York, NY: Dover Publications; 1967.
• 19. Corless RM, Fillion N. A graduate introduction to numerical methods. New York, NY: Springer; 2016.
• 23. Saltelli A, Ratto M, Andres T, Campolongo F, Cariboni J, Gatelli D, et al. Global sensitivity analysis: The primer. Chichester: Wiley; 2008.
• 25. Dietze MC. Ecological forecasting. Princeton, NJ: Princeton University Press; 2017.
• 26. Hobbs NT, Hooten MB. Bayesian models: A statistical primer for ecologists. Princeton, NJ: Princeton University Press

Mathematical modelling: a language that explains the real world

Deputy Director of the DSI-NRF Centre of Excellence in Mathematical and Statistical Sciences and Senior Lecturer in the School of Computer Science and Applied Mathematics, University of the Witwatersrand

Disclosure statement

Ashleigh Jane Hutchinson received funding from the National Research Foundation, South Africa. She is affiliated with the University of the Witwatersrand and the CoE-MaSS, South Africa.

University of the Witwatersrand provides support as a hosting partner of The Conversation AFRICA.

View all partners

The motion of all solid objects and fluids can be described using the unifying language of mathematics. Wind movement , turbulence in the oceans , the migration of butterflies in a big city: all these phenomena can be better understood using mathematics.

Imagine dropping a coin from a tall building. The simple, yet brilliant, result derived by Sir Isaac Newton – that the resultant force equals mass times acceleration – can be used to predict the position of the coin at any given time. The velocity at which the coin reaches the ground can also be calculated with ease. This is a prime example of a mathematical model that can be used to explain what we observe in reality.

Mathematics can be used to solve very complex problems – far more complicated than that of a coin falling under gravity. Industries are in no short supply of such problems. Mathematical techniques can explain how the world works and make it better. Mathematical modelling is capable of saving lives, assisting in policy and decision-making, and optimising economic growth. It can also be exploited to help understand the Universe and the conditions needed to sustain life.

My own work , for example, has involved developing mathematical models for use in industries such as sugar, mining and energy conservation. I’ve worked with researchers from different disciplines to understand the challenges that these industries face, and to help mitigate their effects. This research shows how, far from being simply an abstract area of knowledge, mathematics has many important and practical uses in the real world.

Mining and sugar

For instance, our research in the mining industry deals with roof collapse in underground mines. Such collapses pose a serious concern to the safety of miners, as well as the efficiency of mining operations. It’s important to identify possible sections of a mine roof that may be prone to collapse. That’s where mathematical modelling comes in: with further investigation and research, we can use it to predict roof collapses. Miners can be safely evacuated before something like this happens.

South Africa, where I conduct my research, had a record-low number of deaths due to mining related incidents in 2019. But even a single preventable death is unacceptable. Mathematical modelling can help to inform safety measures and keep the fatality rate down.

The sugar industry has also benefited from mathematical modelling. Manufacturers want to produce as many sugar crystals as possible, in minimal time. We have used mathematical modelling to suggest ways in which the process of separating molasses from the sugar crystals can be speeded up so that the production time of sugar can be optimised.

This work doesn’t just benefit individual sugar producers. In South Africa, the sugar industry not only provides job opportunities, but surplus sugar is also exported . Getting as much of the end product as possible out of the raw materials contributes to the economy by increasing the amount of sugar exported to other countries.

Power predictions

One of the research projects I have been involved with focuses on a very hot topic in South Africa and elsewhere on the African continent: power supply.

A lack of power supply is not only a nuisance in domestic households, it has a fundamental effect on the economy . One of the relevant issues here is what to charge users. Tariffs, which are the price per unit of electricity, are based on numerous factors. High tariff price increases have led to households and businesses investing in renewable energy sources and removing themselves from the grid . Once this happens, less income is available to cross-subsidise the poor, who would otherwise not have access to electricity.

Mathematical modelling can be used to show – as we have done – that increasing tariff prices, which encourages consumers to invest in alternative energy supplies, will lead to exactly the situation described above, putting the country’s state-owned power entity, Eskom, at risk.

This is an example of how mathematical modelling can play a valuable role in informing policy decisions.

Bringing researchers together

Our research also highlights the importance of collaboration in tackling difficult problems in industry.

This is a crucial element of mathematical modelling: it unifies researchers from different academic backgrounds. Developing a mathematical model is really just the start of a research project. Predictions obtained from any mathematical model need to be studied by experts in order to verify whether the model is a valid and accurate representation of the real-world problem of interest. So for instance, our work on the power grid could be assessed by economists to test it against real-world figures, then applied by policy makers.

• Mathematics
• Electricity
• Mathematical modelling

Editorial Internship

Manager, Enterprise Applications

Integrated Management of Invasive Pampas Grass for Enhanced Land Rehabilitation

Deputy Vice-Chancellor (Indigenous Strategy and Services)

A systematic literature review of the current discussion on mathematical modelling competencies: state-of-the-art developments in conceptualizing, measuring, and fostering

• Open access
• Published: 15 October 2021
• Volume 109 , pages 205–236, ( 2022 )

Cite this article

You have full access to this open access article

• Mustafa Cevikbas 1 ,
• Gabriele Kaiser   ORCID: orcid.org/0000-0002-6239-0169 1 , 2 &
• Stanislaw Schukajlow 3  

17k Accesses

61 Citations

6 Altmetric

Explore all metrics

This article has been updated

Mathematical modelling competencies have become a prominent construct in research on the teaching and learning of mathematical modelling and its applications in recent decades; however, current research is diverse, proposing different theoretical frameworks and a variety of research designs for the measurement and fostering of modelling competencies. The study described in this paper was a systematic literature review of the literature on modelling competencies published over the past two decades. Based on a full-text analysis of 75 peer-reviewed studies indexed in renowned databases and published in English, the study revealed the dominance of an analytical, bottom-up approach for conceptualizing modelling competencies and distinguishing a variety of sub-competencies. Furthermore, the analysis showed the great richness of methods for measuring modelling competencies, although a focus on (non-standardized) tests prevailed. Concerning design and offering for fostering modelling competencies, the majority of the papers reported training strategies for modelling courses. Overall, the current literature review pointed out the necessity for further theoretical work on conceptualizing mathematical modelling competencies while highlighting the richness of developed empirical approaches and their implementation at various educational levels.

Similar content being viewed by others

Modelling Competencies: Past Development and Further Perspectives

Fostering Mathematical Modelling Competencies: A Systematic Literature Review

Empirical research on teaching and learning of mathematical modelling: a survey on the current state-of-the-art

Avoid common mistakes on your manuscript.

Modelling and applications are essential components of mathematics, and applying mathematical knowledge in the real world is a core competence of mathematical literacy; thus, fostering students’ competence in solving real-world problems is a widely accepted goal of mathematics education, and mathematical modelling is included in many curricula across the world. Despite this consensus on the relevance of mathematical modelling competencies, various influential approaches exist that define modelling competencies differently. In psychological discourse, competencies are mainly defined as cognitive abilities for solving specific problems, complemented by affective components, such as the volitional and social readiness to use the problem solutions (Weinert, 2001 ). In the mathematics educational discourse, Niss and Højgaard ( 2011 , 2019 ) emphasized cognitive abilities as the core of mathematical competencies within their extensive framework, an updated version of which has recently been published; therefore, the question of how to conceptualize competence as an overall construct, with competency and competencies as associated derivations, remains open.

The discussion on the teaching and learning of mathematical modelling, which began in the 1980s, has emphasized the practical application of mathematical modelling skills; for example, the prologue of the proceedings of the first conference on the teaching and learning of mathematical modelling and applications (hereafter ICTMA) stated: “To become proficient in modelling, you must fully experience it – it is no good just watching somebody else do it, or repeat what somebody else has done – you must experience it yourself” (Burghes, 1984 , p. xiii). This strong connection to proficiency may be one reason for the early development of the discourse on modelling competencies compared to other domains, such as teacher education.

Despite this broad consensus on the importance of modelling competencies and the relevance of the modelling cycle in specifying the expected modelling steps and phases, no worldwide accepted research evidence exists on the effects of short- and long-term mathematical modelling examples and courses in school and higher education on the development of modelling competencies. One reason for this research gap may be the diversity of instruments for measuring modelling competencies and the lack of agreed-upon standards for investigating the effects of fostering mathematical modelling competencies at various educational levels, which depends on reliable and valid measurement instruments. Finally, only a few approaches have addressed or further developed the construct of mathematical modelling competencies and/or its descriptions and components. Precise conceptualizations of mathematical modelling competence as a construct are needed to underpin reliable and valid measurement instruments and implementation studies to foster mathematical modelling competencies effectively.

With this systematic literature review, the results of which are presented in this paper, we aimed to analyze current state-of-the-art research regarding the development of modelling competencies and their conceptualization, measurement, and fostering. This analysis hopefully will contribute to a better understanding of the previously mentioned research gaps and may encourage further research.

1 Theoretical frameworks as the basis for the research questions and analysis

To date, only one comprehensive literature review on modelling competencies—a classical literature search on modelling competencies by Kaiser and Brand ( 2015 )—has been conducted, constituting an important starting point for the current discourse on mathematical modelling. Contrasting with the present systematic literature review using reputable databases, this classical literature review was based on the proceedings of the biennial ICTMA series. A study by the International Commission on Mathematics Instruction (ICMI) on modelling and applications (the 14th ICMI Study), conducted at the International Congress of Mathematical Education’s (ICME’s) international quadrennial congresses, reviewed related books published by special groups, together with special issues of mathematics educational journals and other journal papers. Based on this literature survey, the development of the discourse on modelling competencies since the start of the international conference series in 1983 was reconstructed by Kaiser and Brand ( 2015 ).

The review indicated that the early discourse addressed the constructs of modelling skills or modelling abilities, including metacognitive skills. The first widespread use of the modelling competence construct emerged with the 14th ICMI Study on Applications and Modelling, a separate part of which was devoted to modelling competencies (Blum et al., 2007 ). More or less simultaneously, the discussion on modelling competence, and its conceptualization and measurement, started at ICTMA12 (Haines et al., 2007 ) and continued at ICTMA14 (Kaiser et al., 2011 ), with both proceedings containing sections on modelling competencies.

In their literature review, Kaiser and Brand ( 2015 ) distinguished four central perspectives on mathematical modelling competencies with different emphases and foci. These four perspectives were characterized as follows:

Introduction of modelling competencies and an overall comprehensive concept of competencies by the Danish KOM project (Niss & Højgaard, 2011 , 2019 )

Measurement of modelling skills and the development of measurement instruments by a British-Australian group (Haines et al., 1993 ; Houston & Neill, 2003 )

Development of a comprehensive concept of modelling competencies based on sub-competencies and their evaluation by a German modelling group (Kaiser, 2007 ; Maaß, 2006 )

Integration of metacognition into modelling competencies by an Australian modelling group (Galbraith et al., 2007 ; Stillman, 2011 ; Stillman et al., 2010 ).

These perspectives shaping the discourse on modelling competencies followed two distinct approaches to understanding and defining mathematical modelling competence: a holistic understanding and an analytic description of modelling competencies, referred to as top-down and bottom-up approaches by Niss and Blum ( 2020 ).

In the following, we describe these two diametrically opposite approaches and identify intermediate approaches.

1.1 A holistic approach to mathematical modelling competence—the top-down approach

The Danish KOM project first clarified the concept of modelling competence, which was embedded by Niss and Højgaard ( 2011 ) into an overall concept of mathematical competence consisting of eight mathematical competencies. The modelling competency was defined as one of the eight competencies, which were seen as aspects of a holistic description of mathematical competency, in the sense of Shavelson ( 2010 ). The modelling competency was defined by Niss and Højgaard ( 2011 ) as follows:

This competency involves, on the one hand, being able to analyze the foundations and properties of existing models and being able to assess their range and validity. Belonging to this is the ability to ‘de-mathematise’ (traits of) existing mathematical models; i.e. being able to decode and interpret model elements and results in terms of the real area or situation which they are supposed to model. On the other hand, competency involves being able to perform active modelling in given contexts; i.e. mathematising and applying it to situations beyond mathematics itself. (p. 58)

In their revised version of the definition of mathematical competence, Niss and Højgaard ( 2019 ) explicitly excluded affective aspects such as volition and focused on cognitive components. Referring to the mastery of the modelling competency, Blomhøj and Højgaard Jensen ( 2007 ) developed three dimensions for evaluation:

Degree of coverage, referring to the part of the modelling process the students work with and the level of their reflection

Technical level, describing the kind of mathematics students use

Radius of action, denoting the domain of situations in which students perform modeling activities.

Niss and Blum’s ( 2020 ) description of these approaches called this definition the “top-down” definition, referring explicitly to the expression “modelling competency” as singular, denoting a “distinct, recognizable and more or less well-defined entity” (p. 80).

Concerning the fostering of modelling competencies, Blomhøj and Jensen ( 2003 ) distinguished holistic and atomistic approaches. The holistic approach depends on a full-scale modelling process, with the students working through all phases of the modelling process. In the atomistic approach, students concentrate on selected phases of the modelling process, especially the processes of mathematizing and analyzing models mathematically, because these phases are seen as especially demanding. However, the authors issued a strong plea for a balance between these two approaches, since neither of them alone was seen as adequate.

1.2 An analytic approach to modelling competencies and sub-competencies—the bottom-up approach

The analytic definition of competence refers to the seminal work of Weinert ( 2001 ), which described it as “the cognitive abilities and skills available to individuals or learnable through them to solve specific problems, as well as the associated motivational, volitional and social readiness and abilities to use problem solutions successfully and responsibly in variable situations” (Weinert, 2001 , p. 27f). Based on this definition, modelling competencies were distinguished from modelling abilities: “Modelling competencies include, in contrast to modelling abilities, not only the ability but also the willingness to work out problems, with mathematical aspects taken from reality, through mathematical modelling” (Kaiser, 2007 , p. 110). Similarly, Maaß ( 2006 ) described modelling competencies as the ability and willingness to work out problems with mathematical means, including knowledge as the inevitable basis for competencies. The emphasis on knowledge as part of competence is in line with the discussion on competencies in the professional development of teachers; the most recent approach within this discussion on competence as a continuum aims to connect dispositions, including knowledge and beliefs, with situation-specific skills and classroom performance (Blömeke et al., 2015 ). Due to the fact that no standard methods exist for mathematical modelling as a means to find solutions to real-world problems, many cognitive and affective barriers must be overcome. This situation makes metacognitive skills and knowledge needed to monitor modelling activities highly relevant to the development of non-standard approaches. The construct of metacognition has been introduced into the broad discussion about the teaching and learning of mathematical modelling and plays an increasing role within the current modelling discourse, which was called for by Stillman and Galbraith in 1998 and further developed by, among others, Stillman ( 2011 ) and Vorhölter ( 2018 ).

Departing from the developments described above, a distinction has been developed between global modelling competencies and the sub-competencies of mathematical modelling within the mathematical modelling discourse (Kaiser, 2007 ; Maaß, 2006 ). Global modelling competencies are defined as the abilities necessary to perform and reflect on the whole modelling process, to at least partially solve a real-world problem through a model developed by oneself, to reflect on the modelling process using meta-knowledge, and to develop insight into the connections between mathematics and reality and into the subjectivity of mathematical modelling. Furthermore, social competencies, such as the ability to work in groups and communicate about and via mathematics, are part of global competencies.

The sub-competencies of mathematical modelling relate to the modelling cycle, of which different descriptions exist, including the different competencies essential for performing individual steps of the modelling cycle. Based on early work by Blum and Kaiser ( 1997 ) and subsequent extensive empirical studies, the following sub-competencies of modelling competence were distinguished by Kaiser ( 2007 , p. 111) and similarly by Maaß ( 2006 ):

Competencies to understand real-world problems and to develop a real-world model

Competencies to create a mathematical model out of a real-world model

Competencies to solve mathematical problems within a mathematical model

Competencies to interpret the mathematical results in a real-world model or a real-world situation

Competencies to challenge the developed solution and carry out the modelling process again, if necessary

Due to the strong reference to sub-competencies as part of the construct competence, this approach is called the analytic approach or, according to Niss and Blum ( 2020 ), the “bottom-up approach” (p. 80). Stillman et al. ( 2015 ) noted in their summarized description of this perspective the comprehensive character of this approach, referring to the early development of assessment instruments with multiple-choice items mapped to indicators of each sub-competence (e.g., Haines et al., 1993 ), which was adopted by further studies. Additionally, different levels of modelling competence were distinguished based, for example, on various test instruments (Maaß, 2006 ; Kaiser, 2007 ) and metacognitive frameworks (Stillman, 2011 ).

1.3 Further approaches to mathematical modelling competence

Further approaches concerning the construct of mathematical modelling competence can be distinguished, which this section briefly summarizes.

In their survey paper for the ICMI study on mathematical modelling and applications, Niss et al. ( 2007 ) proposed an enrichment of the top-down method, which integrated the main characteristics of the top-down approach with elements of the bottom-up approach. Referring to the holistic approach to competency, they defined mathematical modelling competency as follows:

[The] ability to identify relevant questions, variables, relations or assumptions in a given real world situation, to translate these into mathematics and to interpret and validate the solution of the resulting mathematical problem in relation to the given situation, as well as the ability to analyze or compare given models by investigating the assumptions being made, checking properties and scope of a given model etc. in short: modelling competency in our sense denotes the ability to perform the processes that are involved in the construction and investigation of mathematical models. (p. 12–13)

Furthermore, social competencies and mathematical competencies were included in this approach, which had (at least initially) some similarities to the bottom-up approach; however, with the inclusion of a critical analysis of modelling activities, this approach can be seen as resembling the top-down approach. In our systematic literature review, we call this approach a top-down enriched approach.

Other approaches have also been developed in the past, and hierarchical level-oriented approaches in particular have received some attention; for example, Henning and Keune ( 2007 ) focused on the cognitive demands of modelling competencies and distinguished them as follows: level one recognition and understanding of modelling, level two independent modelling, and level three meta-reflection on modelling. Furthermore, design-based model-eliciting activity principles, which had been developed as assessment tools for modelling competencies, were proposed as competence framework (Lesh et al., 2000 ). Another framework taken up within the discourse was the framework for the successful implementation of mathematical modelling (Stillman et al., 2007 ).

Summarizing the description of the theoretical approaches to mathematical modelling competencies, we can state that only a few established theoretical frameworks currently exist, which are difficult to discriminate between, as they refer to each other and the ongoing discourse. Overall, although modelling competencies are clearly conceptualized, as evidenced by the inclusion of current approaches in the ongoing discussion, we could not identify a rich variety of conceptualizations on which to build our literature review.

1.4 Research questions

Building upon the above-mentioned theoretical frameworks for conceptualizing modelling competencies and ways to measure and foster them, our study systematically reviewed the existing literature in the field of modelling competencies. In order to reveal how cumulative progress has been made in research over the past few decades, we endeavored to answer the following research questions and analyze them over time (i.e., the last three decades):

1.4.1 Study characteristics and research methodologies

How are the studies on modelling competencies distributed, and how can they be characterized by the country of origin of the authors, appearance over time, type of paper (theoretical or empirical; conference proceedings papers or journal papers), use of research methods, educational level involved, previous modelling experience before implementing the study, and type of modelling task used?

1.4.2 Characteristics of the studies concerning the conceptualization, measurement, and fostering of modelling competencies

How have researchers conceptualized modelling competencies? Are the theoretical perspectives identified and described in the theoretical frameworks also reflected in the various empirical studies? Are modelling competencies conceptualized as a holistic construct, or are they further differentiated as analytic constructs using various sub-competencies?

Which instruments for measuring modelling competencies have researchers used to study (preservice) teachers’ or school students’ modelling competencies? Specifically, what types of instruments and data collection methods were used, which groups were targeted, and what were the sample sizes?

Which interventions for fostering and measuring modelling competencies have researchers used to support (preservice) teachers’ or school students’ modelling competencies?

In the following section, we describe the methods used for this literature review before we present the results. The paper closes with an outlook on further perspectives on the work based on this systematic literature review and on the contributions of the papers in this special issue of Educational Studies in Mathematics on modelling competencies.

2 Methodology of the systematic literature review

2.1 search strategies and manuscript selection procedure.

To uncover the current state of the research conceptualizing mathematical modelling competencies and their measurement and fostering, we conducted a systematic literature review. This approach involves “a review of a clearly formulated question that uses systematic and explicit methods to identify, select, and critically appraise relevant research, and to collect and analyze data from the studies that are included in the review” (Moher et al., 2009 , p. 1).

The current review followed the most recent Preferred Reporting Items for Systematic Reviews and Meta-Analysis (PRISMA) guidelines (Page et al., 2021 ). The final literature search was carried out on March 17, 2021 in the following databases: (1) Web of Science (WoS) Core Collection, (2) Scopus, (3) PsycINFO, (4) ERIC, (5) Teacher Reference Center, (6) IEEEXplore Digital Library, (7) SpringerLink, (8) Taylor & Francis Online Journals, (9) zbMATH Open, (10) JSTOR, (11) MathSciNet, and (12) Education Source. These databases have high-quality indexing standards and a high international reputation. Furthermore, they contain many studies in the field of educational sciences, particularly in mathematics education research. In order to capture the relevant studies in the field of mathematics education research, search strings with Boolean operators and asterisks were used in the systematic review, as shown in Table 1 .

The current survey focused on studies conducted in the field of mathematics education, published in English, which closely related to the conceptualization, measurement, or fostering of mathematical modelling competencies. Our search embraced studies conducted at all levels of mathematics education and did not restrict the publication year of the studies. Overall, to specify eligible manuscripts for the review, we used five inclusion and five exclusion criteria as presented in Table 2 ; since not all exclusion criteria were exact opposites of the inclusion criteria, we separated exclusion and inclusion criteria. All the authors of this study were responsible for determining the eligibility of the papers for inclusion.

In addition to the electronic database search, on the basis of the first four criteria (IC1-IC4 and EC1-EC4), we conducted a hand-search for key conference proceedings that are important for mathematical modelling research, although they were not indexed in the electronic databases (amongst others as they were not registered by their publishers). We therefore screened the ICTMA proceedings from 1984 to 2009 and the recently published ICTMA19 proceedings. There was no need to manually screen the remaining ICTMA proceedings since they were already indexed in databases covered by IC5. Hand-searching is an accepted way of identifying the most recent studies that have not yet been included in or indexed by academic databases (Hopewell et al., 2007 ).The manuscript selection process was conducted in three main stages: (1) identification, (2) screening, and (3) inclusion (Page et al., 2021 ). In the identification stage, search strings from Table 1 were used, and a literature search of the 12 listed databases yielded 6,146 records. Endnote served as bibliographic software for managing references and removing duplicate records. After discarding 670 duplicate records, we moved to the initial screening of 5,476 records. Additionally, we found 411 potentially eligible records through hand-searching and screened all 5,887 reports based on their titles, abstracts, and keywords. First, we used the “refine” or “limit to” features of the electronic databases to exclude 3,276 papers by selecting the document type as journal article, book chapter, or conference proceedings; the language as English (all databases); and subject areas as education/educational research and educational scientific disciplines (WoS), education (Taylor & Francis Online Journals, SpringerLink, and JSTOR), social sciences (Scopus), and mathematics (WoS and Scopus). We then manually screened the remaining 2,611 reports’ titles, abstracts, and keywords on the basis of our ICs and ECs and found 204 potentially relevant studies through independent examination by the authors. At the end of the screening stage, we examined the full-text versions of these 204 studies based on our eligibility criteria, as mentioned in Table 2 . Ultimately, we included 75 studies in the systematic review with the full agreement of all the authors. Figure 1 illustrates the flow chart for the entire manuscript selection process.

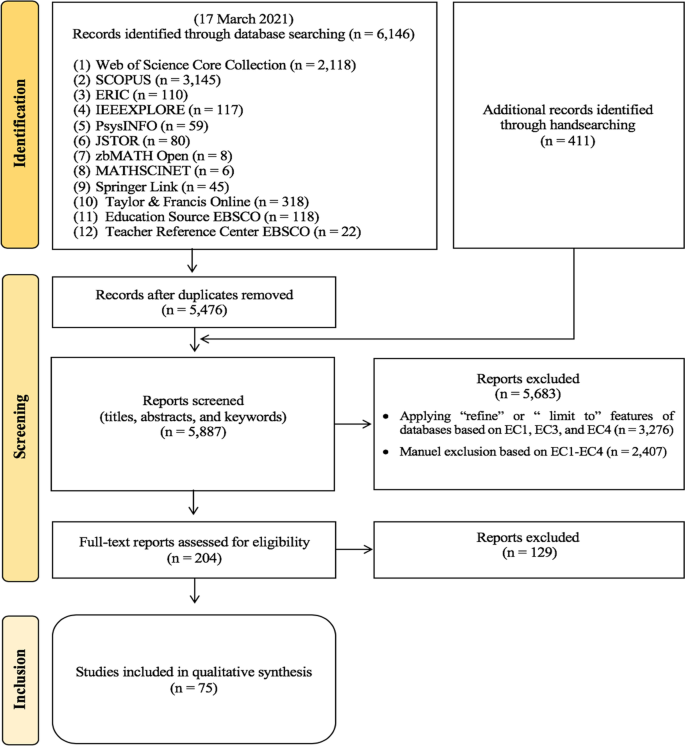
Flow diagram of the manuscript selection process

2.2 Data analysis

Our analysis included 75 papers, which are described in Tables 9 , 10 , 11 , and 12 in the Appendix and displayed in the electronic supplementary material. The analysis of the current review mainly consisted of a screening and a coding procedure. First, the eligible studies were screened three times by the authors and examined in-depth. A coding scheme was then developed, and the codes were structured around our research questions according to four overarching categories:

Study characteristics and research methodologies (research question 1)

Theoretical frameworks for modelling competencies (research question 2)

Measuring mathematical modelling competencies (research question 3)

Fostering mathematical modelling competencies (research question 4)

Table 3 exemplifies our coding concerning the theoretical conceptualization of the reviewed papers.

The analysis was carried out according to the qualitative content analysis method (Miles & Huberman, 1994 ), focusing on the topics the reviewed studies addressed. We analyzed the studies that concerned our research interests, systematized according to the four main categories. First, concerning research question 1, we categorized the general characteristics of the reviewed studies and the research methodologies they had used based on ten sub-categories (e.g., publication year, document type, geographic distribution, research methods, sample/participants, participants’ level of education, sample size, participants’ previous experience in modelling, task types and modelling activities, and data collection methods). Second, with a special focus on research question 2, we analyzed the theoretical frameworks for modelling competencies that motivated the studies. Regarding research questions 3 and 4, we identified the measurement and fostering strategies developed, used, or suggested in the reviewed studies.

The main parts of the coding manual can be found in the Appendix, displayed in the electronic supplementary material (Tables 9 , 10 , 11 , and 12 ) with a sample coding in Table 12 . Our initial coding was conducted by the first author, and multiple strategies were then used to check the coding reliability using Miles and Huberman’s ( 1994 , p.64) formula: “reliability = number of agreements / (total number of agreements + disagreements).” First, we applied a code-recode strategy, which involved recoding all the studies after an interval of four weeks, and the consistency rate between the two distinct coding sessions was computed as 0.97. Second, to test coding reliability, 20% of the reviewed papers were randomly selected and cross-checked for coherence by a coder other than the authors, who had previous experience in mathematical modelling research area and qualitative data analysis. The intercoder reliability was found to be 0.93. Third, the first two authors separately coded the theoretical frameworks of all the included studies because these frameworks for modelling competencies were more complex to code than the other categories due to more interpretative elements. After double coding all the data concerning the theoretical frameworks underpinning the studies, the intercoder reliability rate was 0.91. After applying these strategies, all coders discussed the coding schedule, with a particular focus on the discrepancies between different codes, to achieve full consensus. All the computed reliability rates illustrated that the coding system was sufficiently reliable (Creswell, 2013 ).

3 Results of the systematic literature review on mathematical modelling competencies

3.1 study characteristics and research methodologies of the papers (research question 1), 3.1.1 types of documents and publication years.

The 75 papers included in our study consisted of 67 empirical studies, 4 theoretical studies, 3 survey or overview studies, and 1 document analysis study with the following distribution of papers: 31 journal articles, 42 conference proceedings, and 2 book chapters. Eligible papers were published in 21 different scientific journals, including 10 mathematics education journals, 5 educational journals, and 4 interdisciplinary scientific journals focusing on science, technology, engineering, and mathematics (STEM) education. The reviewed articles published in mathematics education journals constituted only 7% of all the reviewed studies. Concerning conference proceedings, the majority of the eligible papers came from ICTMA proceedings ( n = 31), with only a few studies from other mathematics education conferences (mainly ICME, Psychology in Mathematics Education [PME], and Congress of the European Society for Research in Mathematics Education [CERME]). Concerning publication years, the reviewed studies appeared between 2003 and 2021, and an increase was observed in studies on modelling competencies in 2020 (see Fig. 2 ). The visualization in Fig. 2 does not show steady progress over time, especially regarding the impact of the biennial ICTMA conferences and their subsequently published proceedings. We called papers stemming from the books from the ICTMA conference series as conference proceedings, although the books have not been named like that in the past decade due to their selectivity and rigorous peer-review process carried out.

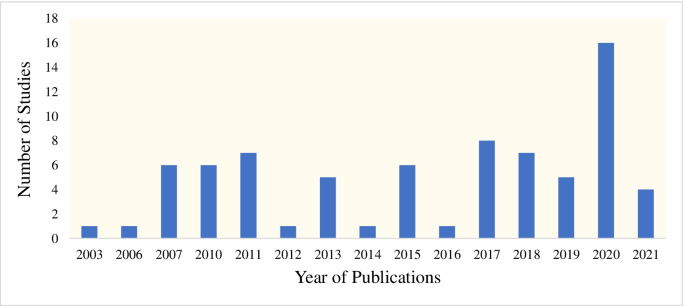
Numbers of annual studies on mathematical modelling competencies

3.1.2 Geographic distribution

The results concerning geographic distribution revealed the contributions of researchers from different countries to research on mathematical modelling competencies. An analysis conducted separately based on all authors’ affiliations and first authors’ affiliations found few important differences; thus, only the results based on all authors’ country affiliations are tabulated. When reviewing the studies, geographical origins were critical, as the classification criteria reflected the research culture of the countries to a certain extent; for example, the competence construct is especially prominent in Europe, whereas in other parts of the world, other constructs, such as proficiency, are more common. We therefore found as expected that most authors came from Europe, followed by Asia, Africa, and America, and only one came from Australia. In particular, the authors came from 18 different countries, with Germany being the most prominent. Table 4 indicates the distribution of the authors by country and continent.

3.1.3 Research designs and data collection methods

The analysis revealed that roughly one-third of the reviewed studies (32%, n = 24) used quantitative research methods (e.g., experimental, quasi-experimental, comparative, correlational research, survey, and relational survey models), followed by qualitative research methods (e.g., case study and grounded theory; 27%, n = 20) and design-based research methods (5%, n = 4). Only one study used both qualitative and quantitative research methods, and another study relied on document analysis. A few theoretical studies (5%, n = 4) and overview/survey studies (4%, n = 3) were counted among the remainder. For 18 eligible studies (24%), it was not possible to identify the research method used.

Various data collection methods were used in the reviewed studies, with (non-standardized) test instruments being the most frequently used method (see Fig. 3 ). The majority of the studies (44 of 75 studies, 59%) used more than one data collection method, whereas 23 studies (31%) used only one method. Seven papers reporting theoretical and overview/survey studies were not applicable to this category. We took into account that data collection might not be restricted to the evaluation of modelling competencies, but could include in addition other constructs, such as beliefs or attitudes.

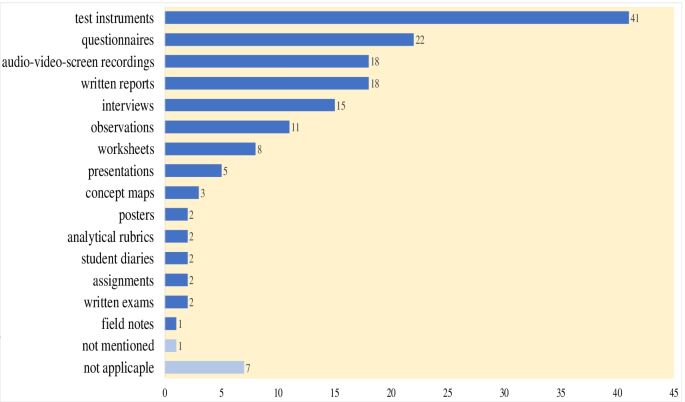
Data collection methods used in the reviewed studies

3.1.4 Focus samples, sample sizes, and study participants’ levels of education

In this review study, we analyzed the sample characteristics of the reviewed studies. When we categorized the participants of the studies, we took into consideration the authors’ reports concerning the educational level of the participants. There is no clear international distinction between elementary and lower secondary education with elementary education covering year 1 to 4 or 1 to 6, which has to be taken into account.

The analysis showed that the majority of the reviewed studies (45%, n = 34) recruited secondary school students (grades 6–12), and 20% ( n = 15) used samples of preservice (mathematics) teachers. Moreover, 12 studies (16%) focused on university students, including engineering students ( n = 8), mathematics and natural science students ( n = 1), and students from an interdisciplinary program ( n = 1), an introductory and interdisciplinary study program in science ( n = 1), and STEM education ( n = 1). Additionally, three studies (4%) used mixed samples of students, preservice teachers, and experienced teachers as their participants. Only two studies (3%) dealt with elementary school students (one group focusing on first graders and the other on fifth graders). One study did not mention the sample. The remaining eight studies (11%) were not applicable to this category, as they did not report on an empirical study or were of a theoretical nature. Figure 4 illustrates the distribution of the reviewed studies’ participants.

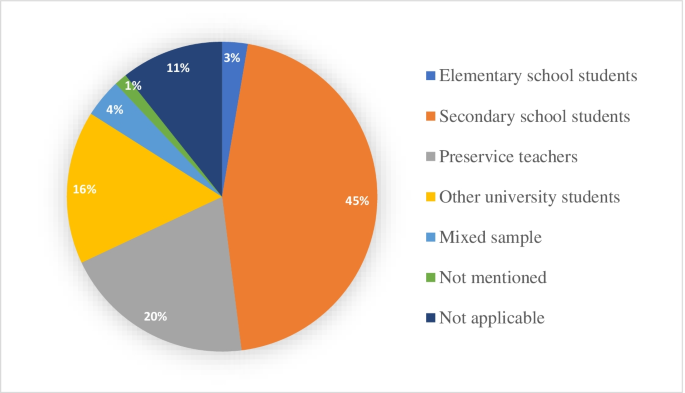
Participants in the reviewed studies

Table 5 shows the analysis of the sample sizes of the studies. The majority of the studies (32%, n = 24) recruited 0-50 participants, and overall, 51% ( n = 38) had less than 200 participants. Additionally, 14 studies (19%) conducted research with 201-500 participants, and 3 large-scale studies (4%) had more than 1,000 participants. We also analyzed the sample sizes of the studies based on the participants’ levels of education, and we used two categories (school/university students and preservice teachers). The results for these two categories did not differ substantially from each other; the most striking difference seemed to be in the range of 201-500 participants who were school students. The table illustrates the difficulties in higher education in collecting data from larger samples.

3.1.5 Participants’ previous modelling experience and modelling task types

Since participants’ previous modelling experience was mentioned as an important factor for success by several studies, we analyzed this information given in the papers. Our results showed that in 25% ( n = 19) of the studies, participants had very limited or no experience in modelling (i.e., they had participated in only one or two modelling activities by the time of the study). Furthermore, two studies reported that their participants had previous modelling experience (e.g., experience gained by attending modelling courses and seminars) before the research interventions. One study mentioned that the participants were heterogeneous in terms of their experience in modelling. Besides these results, we found that the majority of the reviewed studies (65%, n = 45) did not provide any information regarding participants’ previous experience in modelling.

In our review, we also evaluated how modelling activities were carried out during the research interventions and which types of tasks were used by the studies. The results revealed that modelling activities were predominantly performed in group work (37%, n = 28), 5 studies (7%) reported that they guided participants in individual/independent modelling activities, and the other 6 studies (8%) stated that they used both individual and group work. However, numerous reviewed studies (39%, n = 29) did not state how they performed modelling activities.

The types of modelling tasks used in the studies were not clearly described in the majority of the reviewed studies (59%, n = 44). We did not use a predefined classification, but used the classification given by the authors as in many papers no detailed information about the task was provided. This did not allow to use a predefined classification scheme, although we admit the advantages of predefined classifications. In this sense, we found that 11 studies (15%) applied more than 1 task type in the research; however, 18 reviewed studies (24%) employed a single type of modelling task. The results on type of tasks used by the reviewed studies are displayed in Table 6 .

Connected to the low information to the task type is the missing information about the context of the modelling examples (e.g., closeness to students’ world, workplace, citizenship, etc.) in many papers, which did not allow us to analyze this important category.

3.2 Results concerning the theoretical frameworks for modelling competencies (research question 2)

In our review, we classified the theoretical frameworks of the studies for mathematical modelling competencies into six categories. The main approaches used were as described in the theoretical part of this paper, and the results are displayed in Fig. 5 . The most prevalent theoretical framework was the bottom-up approach; other different theoretical frameworks comprised model-eliciting activities and principles as assessment tools for modelling competencies (Lesh et al., 2000 ), level-oriented descriptions of modelling competencies (Henning & Keune, 2007 ), or the framework for success in modelling (Stillman et al., 2007 ). Overall, the results indicated a scarcity of theoretical frameworks underpinning studies that investigated modelling competencies.

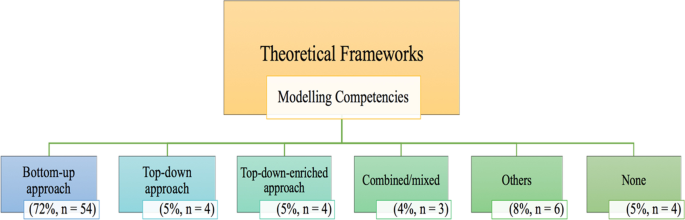
Theoretical frameworks of the studies on modelling competencies

3.3 Results concerning the measurement of modelling competencies (research question 3)

Our results revealed that a number of methods were used to measure modelling competencies. The most prevalent approaches used (mainly non-standardized) test instruments (55%, n = 41), written reports, and audio/video and screen recordings (24%, n = 18). The least-used methods were multidimensional item response theory (IRT) approaches ( n = 1) and field notes ( n = 1). Table 7 illustrates the methods described by the researchers for measuring modelling competencies.

The reviewed studies applied 16 different approaches to measure mathematical modelling competencies: 33% ( n = 25) of the studies used one method, 27% ( n = 20) applied two methods, 17% ( n = 13) used three methods, 7% ( n = 5) followed four methods, 4% ( n = 3) applied 5 methods, and 1 study used 6 different measurement methods for modelling competencies. For one of the reviewed studies, the modelling competency measurement method was not specified.

3.4 Results concerning the fostering of modelling competencies (research question 4)

The analysis revealed that the majority of the reviewed studies (79%, n = 59) contributed to the discourse on fostering modelling competencies by designing, developing, testing, or discussing various activities, including recommendations for the improvement of these activities. The remaining 16 studies (21%) did not mention results about fostering modelling competencies. The activities suggested in the reviewed studies for fostering modelling competencies could be divided into eight groups (see Table 8 ).

In detail, about half of the studies (48%, n = 36) designed and/or used training strategies (e.g., modelling courses/seminars, teaching units, professional development programs, and modelling projects) to foster students’ modelling competencies. Most researchers conducted studies as part of ongoing teaching activities (in schools or universities) or modelling-oriented projects, or they designed specific teaching units aimed at fostering students’ modelling competencies. Concerning modelling tasks, roughly one-third of the studies (31%, n = 23) found that the development of modelling tasks supported students’ modelling competencies. About 9% ( n = 7) of the reviewed studies reported that psychological factors (e.g., motivation, self-efficacy, attitudes, and beliefs) can affect students’ modelling competencies. The analysis revealed that studies found positive correlations between students’ modelling competencies and their levels of self-efficacy and motivation as well as their attitudes and beliefs towards modelling. Moreover, 6 eligible studies (8%) reported that metacognitive factors influenced the modelling competencies of the study participants. A few studies (5%, n = 4) focused on the effects of digital technologies/tools on modelling competencies. The results indicated that using digital devices, such as programmable calculators, special mathematical software (e.g., MATLAB), and dynamic geometry software (e.g., GeoGebra), fostered students’ modelling competencies. Three other eligible studies (4%) discussed the efficiency of the holistic and atomistic approaches to supporting modelling competencies, which we report in detail due to their relevance to the theoretical discourse: The empirical results of these studies illustrated that both approaches foster students’ modelling competencies, although both approaches have weaknesses and strengths. Kaiser and Brand ( 2015 ) found in their comparison of both approaches that the holistic approach had larger effects in interpreting and validating, the atomistic approach had larger effects on working mathematically, and there were mixed results on mathematizing and simplifying. Furthermore, the holistic approach seemed to be more effective than the atomistic approach for students who have relatively weak performance in mathematics (Brand, 2014 ). To summarize, from a developmental perspective, Blomhøj and Jensen ( 2003 ) highlighted the importance of a balance between holistic and atomistic approach to foster students’ modelling competencies.

Seven eligible studies (9%) provided other fostering strategies to develop students’ modelling competencies, as reported in Table 7 .

Overall, the results of the literature review confirmed the richness of the implementation strategies for modelling competencies and emphasized the focus of the current discourse on implementing (or at least suggesting) teaching strategies.

4 Discussion and limitations of the study and further prospects

This review study systematically investigated the current state of research on mathematical modelling competencies through analyzing 75 included papers. Our major focus concerned basic study characteristics, the conceptualization of modelling competencies, and theoretical frameworks and strategies for measuring and fostering modelling competencies.

4.1 Discussion of the results and limitations of the study

Concerning our first research question, our results indicated that the number of reported studies on modelling competencies relatively reached a satisfactory level, with a substantial increase in 2020, but there is still a need for further studies on this topic. Moreover, the vast majority of the reviewed studies were empirical studies, with only a few theoretical or survey studies, and Kaiser and Brand’s ( 2015 ) literature review on modelling competencies, which differed in nature from this one, remains the only other one to date. Conference proceedings, especially ICTMA proceedings, constituted an important proportion of the reviewed studies, followed by journal articles. Notably, the articles published in mathematics education journals accounted for only 7% of the reviewed papers. These results indicate that specialized international mathematics education conferences have a major impact on modelling competence research. Moreover, many articles in high-ranking journals have been written by psychologists rather than mathematics educators, confirming the well-known impression of the low visibility of research on mathematical modelling competencies in mathematics education.

Most authors from reviewed studies came from Europe, particularly Germany; several authors stemmed from Africa and Asia; a very limited number of authors came from North and South America; and only one from Australia. On the one hand, we need to consider the cultural contexts of studies that investigate modelling competencies, and from this point of view, there are plenty of opportunities for future intercultural research on modelling competencies. On the other hand, these results might be influenced by the fact that the competence discussion has been strongly guided by European, especially German, scholars, and that in other discourses, other terminology (e.g., performance, proficiency, skill, and ability) may be used. Further studies should focus on how modelling competencies are conceptualized and identified and consider the terms used for modelling competencies, thus enabling studies to identify the differences or similarities between different approaches to modelling competencies across different countries or cultures. Our review study illustrates that the ICTMA conferences have an influence on the distribution of the papers in terms of country affiliations of the authors. For example, ICTMA18 conducted in Cape Town (South Africa) had a great influence on the number of reviewed papers from South Africa; however, there is no similar effect for South American papers following the ICTMA16 conference held in Blumenau (Brazil), probably reflecting other theoretical perspectives such as socio-cultural approaches, in which modelling competencies play a less pronounced role (Kaiser & Sriraman, 2006 ). Furthermore, institutional restrictions may play an important role concerning the differences in country distribution of these studies.

Our results revealed that approximately one-third of the reviewed studies relied on quantitative research methods, followed by qualitative and design-based research methods. No researcher had named their study approach as mixed-methods research, but only one author reported that both quantitative and qualitative research methods were used. Overall, it is promising that the reviewed studies used a wide variety of data collection methods and more than half of them applied more than one data collection approach, which supports the development of a reliable database (Cevikbas & Kaiser, 2021 ). Moreover, a significant number of the studies focused on secondary school students as participants, followed by preservice teachers and university students from engineering, STEM, and interdisciplinary study programs. However, only two studies recruited elementary school students as participants. In line with these results, the majority of the studies were conducted in secondary education, followed by higher education, but no studies investigated early childhood education or adult education. These results showed that research is needed on modelling competencies in these areas (i.e., early childhood education, elementary education, and adult education).

Notably, interpreting study results regarding students’ modelling competencies crucially depends on knowing the participants’ previous modelling experience, but the majority of the studies provided no information about their participants’ experience in modelling. Additionally, a quarter of the studies reported that their participants had either extremely limited or no experience in modelling, and only two studies stated that their participants had substantial previous experience in mathematical modelling. These results imply that teachers and teacher educators should put great effort into developing students’ modelling experience during their school and university education. Overall, it seems advisable to share information concerning the study participants’ previous experience in modelling to enable readers to make accurate inferences from the study results and compare the results of different studies.

Furthermore, our results indicated that many reviewed studies did not mention which type of task they had used. The analysis of the remaining studies showed that various types of modelling tasks had been implemented. As the core of modelling activities are the modelling tasks or problems, it is crucial to know for the modelling discourse, which modelling tasks are used in studies and what their characteristics are. Using diverse types of modelling tasks can allow researchers to investigate the strengths and weaknesses of these tasks for teaching and learning mathematical modelling and for the promotion of students’ modelling competencies. Using different types of tasks can provide rich opportunities in the learning and teaching of modelling. Further studies should investigate which types of tasks are most effective for developing students’ modelling competencies and should make recommendations for teachers or teacher educators.

Concerning the theoretical frameworks, the results indicated that the predominant framework used by the studies was the bottom-up approach and only a few studies adopted top-down or top-down enriched approaches or other frameworks. Therefore, there is a great need to investigate modelling competencies using a variety of theoretical frameworks and to extend existing frameworks by using innovative approaches. The lack of diversity within the frameworks used directly relates to the conceptualization of modelling competencies; therefore, more theoretical research focusing on the conceptualization of modelling competencies is needed.

The strategies of the reviewed studies for measuring modelling competencies were aligned with their research methods; hence, the results showed that modelling competencies tended to be measured using (mainly non-standardized) test instruments and questionnaires. It is promising that the reviewed studies used various approaches to measure modelling competencies; however, we could not identify any study investigating which method or strategy was most effective for measuring the modelling competencies of students (e.g., focusing on the strengths and weaknesses of different measurement approaches and comparing the capabilities of these approaches to measure students’ modelling competencies). Future studies should focus on producing new tools or strategies to extend existing approaches to measuring students’ modelling competencies by, for example, using digital technologies to measure students’ modelling competencies according to these technologies’ pedagogical potential.

Although the studies reported that students’ or preservice teachers’ mathematical modelling competencies were still far from reaching an expert level, their modelling competencies could be fostered by the various strategies mentioned above (see Results 3.4). In this vein, the reviewed studies contributed to the discourse on fostering modelling competencies by designing, developing, testing, or recommending specific modelling activities. To foster students’ modelling competencies, most of the reviewed studies used instructional strategies that focused on practice in modelling and gaining experience through modelling tasks.

Moreover, several studies found that motivation, self-efficacy, beliefs, and attitudes regarding modelling, and metacognitive competencies, could affect students’ modelling competencies. A few of the studies recommended maintaining a balance between holistic and analytic approaches in the teaching and learning of modelling. Furthermore, few studies have analyzed the use of digital technologies/tools to promote students’ modelling competencies. Accordingly, using mathematical software (e.g., MATLAB and GeoGebra) for modelling has been identified as an effective strategy for fostering modelling competencies, but only a limited number of studies have focused on how and what types of technologies could be used to improve students’ modelling competencies.

In summary, we emphasize that the main foci of this systematic review (i.e., the conceptualization of modelling competencies and the related theoretical frameworks for measuring and fostering modelling competencies) are closely interrelated. Fostering and measuring strategies for modelling competency depend on its conceptualization. To this end, theoretical and empirical studies could contribute strongly to both the epistemology of modelling and its application and are greatly needed.

The results of our systematic literature review are limited by several restrictions. The first significant limitation relates to the restrictions of the databases: The exclusion of papers published in books and journals not included in WoS, Scopus, and the other high-ranking databases led to the exclusion of local/national journals that may have had the potential to provide interesting research studies. Furthermore, the exclusion of papers not written in English excluded many potentially interesting papers, especially those from the Spanish/Portuguese-speaking countries. Further research should try to overcome this limitation by including native speakers from this language area.

Other restrictions related to the automated selection process (i.e., the so-called jingle-jangle fallacy; Gonzalez et al., 2021 ). In our systematic literature review, we used the terms modelling and competence; however, we identified studies that used modelling competence differently, particularly regarding the use of modelling competencies in psychometric or educational modelling (large-scale studies) or in economics or engineering. Manual screening could help overcome this problem; however, we could not prevent the omission of papers that examined modelling competencies but used different terms, such as modelling performance or modelling proficiency. We therefore might have missed an important number of studies that employed other terminology. This is a systemic problem of our approach. Further studies should use a broader theoretical framework to identify and examine these other types of studies.

4.2 Contributions of this special issue to the discourse on modelling competencies

With this present special issue, which the current systematic literature review introduces, we aim to present advances in the research on mathematical modelling competencies. A broad body of past research has investigated modelling processes and students’ barriers to solving modelling problems. Descriptive analyses of students’ solution processes have identified the importance of specific sub-processes and related sub-competencies, such as comprehension, structuring, simplifying, mathematizing, interpretation of mathematical results, and validation of mathematical results and mathematical models for mathematical modelling. However, only a limited amount of research has investigated the effects of short- and long-term interventions on the implementation of mathematical modelling in schools and higher education institutes using rigorous methodological standards. These observations are consistent with the systematic review presented in the previous section, which identified only a limited number of studies contributing to these research aims. In line with these considerations, we argue that much more research effort should be devoted to evaluating measurement instruments and approaches to fostering mathematical modelling in schools and universities (Schukajlow et al., 2018 ). The papers in this special issue contribute to closing these significant gaps by addressing (1) the measurement and (2) the fostering of modelling competencies as well as (3) comparing groups of participants with different expertise or participants from different cultures.

The first group of papers presented assessment instruments for measuring modelling competencies. Based on their conceptualization of modelling competencies, Brady and Jung developed an assessment instrument for analyzing classroom modelling cultures. Their quantitative analysis of the modelling activities of secondary school students demonstrated differences between classroom cultures and revealed shifts in cultures within a classroom, and their qualitative analysis of students’ discourse during presentations of their solutions in classrooms offered an explanation for the phenomenon identified by the quantitative analysis. Brady and Jung interpreted these results as indicative of the validity of the measurement instrument. The new contribution of this study laid in pointing out the importance of using this new assessment instrument to analyze classroom modelling cultures in future studies.

Noticing competencies during mathematical modelling is considered important for research on modelling and on teachers’ situation-specific competencies. Alwast and Vorhölter answered the call to be more specific in the assessment of teachers’ competencies and focused on situation-specific modelling competencies in their study. Alwast and Vorhölter developed staged videos and used these videos as prompts for the assessment of preservice teachers’ noticing competencies in mathematical modelling. They performed a series of studies that aimed to collect evidence of the validity of the new instrument. This instrument could be used in the future to analyze the development of preservice teachers’ noticing skills and to examine the relationship between teachers’ noticing and their decisions and interventions in classrooms.

Students’ creativity, as a research field with a long tradition, has rarely been analyzed in relation to mathematical modelling competencies in the past. Lu and Kaiser identified the importance of creativity for the assessment of modelling competencies and evaluated students’ creative solutions to modelling problems by analyzing three central dimensions of mathematical creativity: usefulness, fluency, and originality. Their analysis of upper secondary school students’ responses indicated a close association between fluency and originality, which has important theoretical implications for the assessment of modelling competencies and the relationship between factors that contribute to mathematical creativity.

The second group of papers examined various approaches to fostering modelling sub-competencies. Geiger, Galbraith, and Niss developed a task design and implementation framework for mathematical modelling tasks aimed at supporting the instructional modelling competence of in-service teachers. The core of this approach was researcher-teacher collaboration over a long period. The results of this study have theoretical implications for implementation research by connecting the task design and task implementation streams of research in a joint model. Furthermore, this research extended the concept of pedagogical competence from numeracy to mathematical modelling competence.

Reading comprehension is an essential part of modelling processes, and improving reading comprehension can help to foster modelling competencies. Krawitz, Chang, Yang, and Schukajlow analyzed the effects of reading comprehension prompts on competence to construct a real-world model of the situation and interest of secondary school students in Germany and Taiwan. Reading comprehension prompts did not affect modelling, but they did affect interest. In-depth analysis of students’ responses indicated a positive relationship between reading comprehension and modelling. Krawitz et al. suggested that the high-quality responses to reading prompts are essential for modelling and should be given more attention in research and practice.

Teaching methods and their impact on the modelling competencies and attitudes of engineering students were the focus of the contribution by Durandt, Blum, and Lindl. The researchers analyzed the effects of independence-oriented and teacher-guided teaching styles in South Africa. The group of students taught according to the independence-oriented teaching style had the strongest competency growth and reported more positive attitudes after the treatment. Students’ independent work supported by adaptive teacher interventions and by a metacognitive scaffold, which encourage individual solutions, is a promising approach that should be analyzed in future studies and evaluated in teaching practice for mathematical modelling competencies.

Greefrath, Siller, Klock, and Wess investigated the effects of two teaching interventions on preservice secondary teachers’ pedagogical content knowledge for teaching mathematical modelling. Preservice teachers in one group designed modelling tasks for use with students, and those in another group were trained to support mathematical modelling processes. Both groups improved some facets of pedagogical content knowledge compared to a third group that received no modelling intervention. As one practical implication of the study, Greefrath et al. underlined the importance of practical sessions for improving preservice teachers’ pedagogical content knowledge of modelling.

The third group of papers included two contributions to comparative studies and a commentary. Preservice teachers’ professional modelling competencies are essential for the teaching of modelling. Yang, Schwarz, and Leung compared this construct in Germany, Mainland China, and Hong Kong. The results indicated that preservice teachers in Germany had higher levels of mathematical content knowledge and mathematical pedagogical knowledge of modelling. Yang et al. suggested that possible reasons for these results might lie in the history of mathematical modelling in mathematics curricula, teacher education, and the teaching cultures in these three regions. Future research should pay more attention to international comparative studies regarding modelling competencies.

Cai, LaRochelle, Hwang, and Kaiser compared expert and novice (preservice) secondary teachers’ competencies in noticing students’ thinking about modelling. The expert teachers noticed the students’ needed to make assumptions to complete the task more often than the novice teachers did. The researchers identified many important characteristics of the differences between experts and novices. Future research should analyze the development of preservice teachers’ and experts teachers’ competencies for noticing students’ thinking about modelling and identify what components of noticing affect the teaching of mathematical modelling competencies.

Finally, Frejd and Vos analyzed the contributions of the papers in this special issue and reflected on further developments in a commentary paper.

Summarizing the contributions of the systematic literature survey and the papers in this special issue, we recognize––despite certain limitations––many insights offered by the special issue that can enhance the current discourse on mathematical modelling competencies. The papers point to a great need for further theoretical work on the conceptualization of modelling competencies, although most papers have adopted a clear theoretical framework in their study. The low number of theoretical papers in this area strongly confirms the need for approaches that have the potential to further develop the current theoretical frameworks, especially taking socio-cultural and socio-critical aspects into account (Maass et al., 2019 ). Furthermore, the development of more standardized test instruments should be encouraged, and an exchange of these instruments within the modelling community (similar to the tests developed by Haines et al., 1993 ) is desirable. In addition, the inclusion of qualitatively oriented, in-depth studies within quantitative studies, leading to mixed-methods designs, seems to be highly desirable. Concerning teachers’ professional competencies, it seems essential to use more recent approaches to competence development, such as developing situation-specific noticing skills of preservice teachers, which should be included in further studies. Scaling-up of established learning environments within implementations under controlled conditions (e.g., by laboratory studies) seems to be highly necessary in order to strengthen the link to psychological research in this area. Despite the high methodological standards in the studies examined in the systematic literature survey and in this special issue, more studies with rigorous methodological standards that rely on the theory of modelling competencies seem to be necessary. One theoretical prediction is that knowledge about modelling and the modelling cycle is a prerequisite for developing modelling competencies. In earlier research, students’ knowledge (e.g., their procedural and conceptual knowledge of modelling as addressed by Achmetli et al., 2019 ) was analyzed as a decisive factor. Future research should assess the various facets of teachers’ modelling competence in relation to its overall construct and students’ modelling competence to contribute to the validation of theories of modelling competencies.

Change history

25 february 2022.

The original version of this paper was updated to add the missing compact agreement Open Access funding note.

Asterisk denotes inclusion in the database.

Achmetli, K., Schukajlow, S., & Rakoczy, K. (2019). Multiple solutions to solve real-world problems and students’ procedural and conceptual knowledge. International Journal of Science and Mathematics Education, 17 , 1605–1625.

Article   Google Scholar  

*Alpers, B. (2017). The mathematical modelling competencies required for solving engineering statics assignments. In G. A. Stillman, W. Blum, & G. Kaiser (Eds.), Mathematical Modelling and Applications. Crossing and Researching Boundaries in Mathematics Education (pp. 189–199). Springer.

*Anhalt, C. O., Cortez, R., & Bennett, A. B. (2018). The emergence of mathematical modelling competencies: An investigation of prospective secondary mathematics teachers. Mathematical Thinking and Learning, 20 (3), 202–221.

*Aydin-Güç, F., & Baki, A. (2019). Evaluation of the learning environment designed to develop student mathematics teachers’ mathematical modelling competencies. Teaching Mathematics and its Applications, 38 (4), 191–215.

*Bali, M., Julie, C., & Mbekwa, M. (2020). Occurrences of mathematical modelling competencies in the nationally set examination for mathematical literacy in South Africa. In G. A. Stillman, G. Kaiser, & C. E. Lampen (Eds.), Mathematical Modelling Education and Sense-making (pp. 361–370). Springer.

*Beckschulte, C. (2020). Mathematical modelling with a solution plan: An intervention study about the development of grade 9 students’ modelling competencies. In G. A. Stillman, G. Kaiser, & C. E. Lampen (Eds.), Mathematical Modelling Education and Sense-making (pp. 129–138). Springer.

*Biccard, P., & Wessels, D. (2017). Six principles to assess modelling abilities of students working in groups. In G. A. Stillman, W. Blum, & G. Kaiser (Eds.), Mathematical Modelling and Applications. Crossing and Researching Boundaries in Mathematics Education (pp. 589–599). Springer.

*Biccard, P., & Wessels, D. C. (2011). Documenting the development of modelling competencies of grade 7 mathematics students. In G. Kaiser, W. Blum, R. Borromeo Ferri, & G. Stillman (Eds.), Trends in Teaching and Learning of Mathematical Modelling, (ICTMA 14 ) (pp. 375–383). Springer.

*Blomhøj, M. (2020).Characterising modelling competency in students’ projects: Experiences from a natural science bachelor program. In G. A. Stillman, G. Kaiser, & C. E. Lampen (Eds.), Mathematical Modelling Education and Sense-making, (pp. 395–405). Springer.

*Blomhøj, M., & Højgaard Jensen, T. (2007). What’s all the fuss about competencies? Experiences with using a competence perspective on mathematics education to develop the teaching of mathematical modelling. In W. Blum, P. L. Galbraith, H. W. Henn, & M. Niss (Eds.), Modelling and Applications in Mathematics Education. The 14th ICMI study (pp. 45–56). Springer.

*Blomhøj, M., & Jensen, T. H. (2003). Developing mathematical modelling competence: Conceptual clarification and educational planning. Teaching Mathematics and its Applications, 22 (3), 123–139.

*Blomhøj, M., & Kjeldsen, T. H. (2010). Mathematical modelling as goal in mathematics education-developing of modelling competency through project work. In B. Sriraman, L. Haapasalo, B. D. Søndergaard, G. Palsdottir, S. Goodchild, & C. Bergsten (Eds.), The first sourcebook on Nordic research in mathematics education (pp. 555–568). Information Age Publishing.

Blömeke, S., Gustaffsson, J. E., & Shavelson, R. (2015). Beyond dichotomies: Viewing competence as a continuum. Zeitschrift für Psychologie, 223 (1), 3–13.

*Blum, W. (2011). Can modelling be taught and learnt? Some answers from empirical research. In G. Kaiser, W. Blum, R. Borromeo Ferri, & G. Stillman (Eds.), Trends in Teaching and Learning of Mathematical Modelling, (ICTMA 14 ) (pp. 15–30). Springer.

Blum, W., Galbraith, P. L., Henn, H. W., & Niss, M. (Eds.). (2007). Modelling and applications in mathematics education, the 14th ICMI Study . Springer.

Google Scholar  

Blum, W., & Kaiser, G., (1997). Vergleichende empirische Untersuchungen zu mathematischen Anwendungsfähigkeiten von deutschen und englischen Lernenden. Unpublished application to German Research Association (DFG).

*Brand, S. (2014). Effects of a holistic versus an atomistic modelling approach on students' mathematical modelling competencies. In P. Liljedahl, C. Nicol, S. Oesterle, & D. Allan (Eds.), Proceedings of the Joint Meeting of PME 38 and PME-NA 36 (Vol. 2, pp. 185–192). PME.

Burghes, D. N. (1984). Prologue. In J. S. Berry, D. N. Burghes, I. D. Huntley, D. J. G. James, & O. Moscardini (Eds.), Teaching and applying mathematical modelling (pp. xi–xvi). Horwood.

Cevikbas, M., & Kaiser, G. (2021). A systematic review on task design in dynamic and interactive mathematics learning environments (DIMLEs). Mathematics, 9 (4), 399. https://doi.org/10.3390/math9040399  

*Cosmes Aragón, S. E., & Montoya Delgadillo, E. (2021). Understanding links between mathematics and engineering through mathematical modelling—The case of training civil engineers in a course of structural analysis. In F. K. S. Leung, G. A. Stillman, G. Kaiser, & K. L. Wong (Eds.), Mathematical Modelling Education in East and West (pp. 527–538). Springer.

Creswell, J. W. (2013). Qualitative inquiry and research design; choosing among five approaches . Sage.

*Czocher, J. A., Kandasamy, S. S., & Roan, E. (2021). Design and validation of two measures: Competence and self-efficacy in mathematical modelling. In A. I. Sacristán, J. C. Cortés-Zavala, & P. M. Ruiz-Arias (Eds.), Mathematics Education Across Cultures: Proceedings of the 42nd Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (pp. 2308–2316). PME-NA. https://doi.org/10.51272/pmena.42.2020

*de Villiers, L., & Wessels, D. (2020). Concurrent development of engineering technician and mathematical modelling competencies. In G. A. Stillman, G. Kaiser, & C. E. Lampen (Eds.), Mathematical Modelling Education and Sense-making (pp. 209–219). Springer.

*Djepaxhija, B., Vos, P., & Fuglestad, A. B. (2017). Assessing mathematizing competences through multiple-choice tasks: Using students’ response processes to investigate task validity. In G. Stillman, W. Blum, & G. Kaiser (Eds.), Mathematical Modelling and Applications. Crossing and Researching Boundaries in Mathematics Education (pp. 601–611). Springer.

*Durandt, R., Blum, W., & Lindl, A. (2021). How does the teaching design influence engineering students’ learning of mathematical modelling? Acase study in a South African context. In F. K. S. Leung, G. A. Stillman, G. Kaiser, & K. L. Wong (Eds.), Mathematical Modelling Education in East and West (pp. 539–550). Springer.

*Durandt, R., & Lautenbach, G. (2020). Strategic support to students’ competency development in the mathematical modelling process: A qualitative study. Perspectives in Education, 38 (1), 211–223.

*Durandt, R., & Lautenbach, G. V. (2020). Pre-service teachers’ sense-making of mathematical modelling through a design-based research strategy. In G. A. Stillman, G. Kaiser, & C. E. Lampen (Eds.), Mathematical Modelling Education and Sense-making (pp. 431–441). Springer.

*Engel, J., & Kuntze, S. (2011). From data to functions: Connecting modelling competencies and statistical literacy. In G. Kaiser, W. Blum, R. Borromeo Ferri, & G. Stillman (Eds.), Trends in Teaching and Learning of Mathematical Modelling, (ICTMA 14 ) (pp. 397–406). Springer.

*Fakhrunisa, F., & Hasanah, A. (2020). Students’ algebraic thinking: A study of mathematical modelling competencies. Journal of Physics: Conference Series, 1521 (3), 032077.

*Frejd, P. (2013). Modes of modelling assessment—A literature review. Educational Studies in Mathematics, 84 (3), 413–438.

*Frejd, P., & Ärlebäck, J. B. (2011). First results from a study investigating Swedish upper secondary students’ mathematical modelling competencies. In G. Kaiser, W. Blum, R. Borromeo Ferri, & G. Stillman (Eds.), Trends in Teaching and Learning of Mathematical Modelling, (ICTMA 14 ) (pp. 407–416). Springer.

Galbraith, P. L., Stillman, G., Brown, J., & Edwards, I. (2007). Facilitating middle secondary modelling competencies. In C. Haines, P. Galbraith, W. Blum, & S. Khan (Eds.), Mathematical Modelling (ICTMA 12): Education, Engineering and Economics (pp. 130–140). Horwood.

Chapter   Google Scholar  

*Gallegos, R. R., & Rivera, S. Q. (2015). Developing modelling competencies through the use of technology. In G. A. Stillman, W. Blum, & M. S. Biembengut (Eds.), Mathematical Modelling in Education Research and Practice (pp. 443–452). Springer.

Gonzalez, O., MacKinnon, D. P., & Muniz, F. B. (2021). Extrinsic convergent validity evidence to prevent jingle and jangle fallacies. Multivariate Behavioral Research, 56 (1), 3–19.

*Govender, R. (2020). Mathematical modelling: A‘growing tree’ for creative and flexible thinking in pre-service mathematics teachers. In G. A. Stillman, G. Kaiser, & C. E. Lampen (Eds.), Mathematical Modelling Education and Sense-making (pp. 443–453). Springer.

*Greefrath, G. (2020). Mathematical modelling competence. Selected current research developments. Avances de Investigación en Educación Matemática, 17 , 38–51.

*Greefrath, G., Hertleif, C., & Siller, H. S. (2018). Mathematical modelling with digital tools—A quantitative study on mathematising with dynamic geometry software. ZDM – Mathematics Education, 50 (1), 233–244.

*Große, C. S. (2015). Fostering modelling competencies: Benefits of worked examples, problems to be solved, and fading procedures. European Journal of Science and Mathematics Education, 3 (4), 364–375.

*Grünewald, S. (2013). The development of modelling competencies by year 9 students: Effects of a modelling project. In G. A. Stillman, G. Kaiser, W. Blum, & J. P. Brown (Eds.), Teaching Mathematical Modelling: Connecting to Research and Practice (pp. 185–194). Springer.

*Hagena, M. (2015). Improving mathematical modelling by fostering measurement sense: An intervention study with pre-service mathematics teachers. In G. A. Stillman, W. Blum, & M. S. Biembengut (Eds.), Mathematical Modelling in Education Research and Practice (pp. 185–194). Springer.

*Hagena, M., Leiss, D., & Schwippert, K. (2017). Using reading strategy training to foster students’ mathematical modelling competencies: Results of a quasi-experimental control trial. Eurasia Journal of Mathematics, Science and Technology Education, 13 (7b), 4057–4085.

Haines, C., Galbraith, P., Blum, W., & Khan, S. (2007). Mathematical modelling (ICTMA 12): Education, engineering and economics . Horwood.

Book   Google Scholar  

Haines, C., Izard, J., & Le Masurier, D. (1993). Modelling intensions realized: Assessing the full range of developed skills. In T. Breiteig, I. Huntley, & G. Kaiser-Messmer (Eds.), Teaching and Learning Mathematics in Context (pp. 200–211). Ellis Horwood.

*Hankeln, C. (2020).Validating with the use of dynamic geometry software. In G. A. Stillman, G. Kaiser, & C. E. Lampen (Eds.), Mathematical Modelling Education and Sense-making (pp. 277–286). Springer.

*Hankeln, C., Adamek, C., & Greefrath, G. (2019). Assessing sub-competencies of mathematical modelling—Development of a new test instrument. In G. A. Stillman, & J. P. Brown (Eds.), Lines of Inquiry in Mathematical Modelling Research in Education, ICME-13 Monographs (pp. 143–160). Springer.

*Henning, H., & Keune, M. (2007). Levels of modelling competencies. In W. Blum, P. L. Galbraith, H. W. Henn, & M, Niss (Eds.), Modelling and Applications in Mathematics Education, the 14th ICMI Study (pp. 225–232). Springer.

*Hidayat, R., Zamri, S. N. A. S., & Zulnaidi, H. (2018). Does mastery of goal components mediate the relationship between metacognition and mathematical modelling competency? Educational Sciences: Theory & Practice, 18 (3), 579–604.

*Hidayat, R., Zamri, S. N. A., Zulnaidi, H., & Yuanita, P. (2020). Meta-cognitive behaviour and mathematical modelling competency: Mediating effect of performance goals. Heliyon, 6 (4), e03800.

*Hidayat, R., Zulnaidi, H., & Syed Zamri, S. N. A. (2018). Roles of metacognition and achievement goals in mathematical modelling competency: A structural equation modelling analysis. PloS One, 13 (11), e0206211.

*Højgaard, T. (2010). Communication: The essential difference between mathematical modelling and problem solving. In R. Lesh, P. L. Galbraith, C. R. Haines, & A. Hurford (Eds.), Modelling Students’ Mathematical Modelling Competences . Springer.

Hopewell S, Clarke M, Lefebvre C, & Scherer R. (2007). Handsearching versus electronic searching to identify reports of randomized trials. Cochrane Database of Systematic Reviews, 2, MR000001. https://doi.org/10.1002/14651858.MR000001.pub2

Houston, K., & Neil, N. (2003). Assessing modelling skills. In S. Lamon, W. Parker, & K. Houston (Eds.), Mathematical Modelling: A Way of Life (pp. 165–178). Horwood.

*Huang, C. H. (2011). Assessing the modelling competencies of engineering students. World Transactions on Engineering and Technology Education, 9 (3), 172–177.

*Huang, C. H. (2012). Investigating engineering students’ mathematical modelling competency from a modelling perspective. World Transactions on Engineering and Technology Education, 10 (2), 99–104.

*Ikeda, T. (2015). Applying PISA ideas to classroom teaching of mathematical modelling. In K. Stacey, & R. Turner (Eds.), Assessing Mathematical Literacy: The PISA Experience (pp. 221–238). Springer.

*Jensen, T. H. (2007). Assessing mathematical modelling competency. In C. Haines, P. Galbraith, W. Blum, & S. Khan (Eds.), Mathematical Modelling (ICTMA 12): Education, Engineering and Economics (pp. 141–148). Horwood.

*Julie, C. (2020). Modelling competencies of school learners in the beginning and final year of secondary school mathematics. International Journal of Mathematical Education in Science and Technology , 51 (8), 1181–1195.

*Kaiser, G. (2007). Modelling and modelling competencies in school. In C. Haines, P. Galbraith, W. Blum, & S. Khan (Eds.), Mathematical Modelling (ICTMA 12): Education, Engineering and Economics (pp. 110–119). Horwood.

Kaiser, G. (2017). The teaching and learning of mathematical modelling. In J. Cai (Ed.), Compendium for Research in Mathematics Education (pp. 267–291). National Council of Teachers of Mathematics.

Kaiser, G., Blum, W., Borromeo Ferri, R., & Stillman, G. (2011). Trends in teaching and learning of mathematical modelling, (ICTMA 14) . Springer.

*Kaiser, G., & Brand, S. (2015). Modelling competencies: Past development and further perspectives. In G. A. Stillman, W. Blum, & M. S. Biembengut (Eds.), Mathematical Modelling in Education Research and Practice (pp. 129–149). Springer.

*Kaiser, G., & Maaß, K. (2007). Modelling in lower secondary mathematics classroom—Problems and opportunities. In W. Blum, P. L. Galbraith, H. W. Henn, & M, Niss (Eds.), Modelling and Applications in Mathematics Education, the 14th ICMI Study (pp. 99–108). Springer.

Kaiser, G., & Sriraman, B. (2006). A global survey of international perspectives on modelling in mathematics education. ZDM – Mathematics Education, 38 (3), 302–310.

*Keisar, E., & Peled, I. (2018). Investigating new curricular goals: What develops when first graders solve modelling tasks? Research in Mathematics Education , 20 (2), 127–145.

*Kreckler, J. (2017). Implementing modelling into classrooms: Results of an empirical research study. In G. A. Stillman, W. Blum, & G. Kaiser (Eds.), Mathematical Modelling and Applications . Crossing and Researching Boundaries in Mathematics Education (pp. 277–287). Springer.

*Krüger, A., Vorhölter, K., & Kaiser, G. (2020). Metacognitive strategies in group work in mathematical modelling activities–The students’ perspective. In G. A. Stillman, G. Kaiser, & C. E. Lampen (Eds.), Mathematical Modelling Education and Sense-making (pp. 311–321). Springer.

*Leiss, D., Schukajlow, S., Blum, W., Messner, R., & Pekrun, R. (2010). The role of the situation model in mathematical modelling—Task analyses, student competencies, and teacher interventions. Journal für Mathematik-Didaktik, 31 (1), 119–141.

*Leong, K. E., & Tan, J. Y. (2020). Exploring secondary students’ modelling competencies. The Mathematics Enthusiast , 17 (1), 85–107.

Lesh, R., Hoover, M., Hole, B., Kelly, A., & Post, T. (2000). Principles for developing thought revealing activities for students and teachers. In A. Kelly & R. A. Lesh (Eds.), Handbook of Research Design in Mathematics and Science Education (pp. 591–645). Lawrence Erlbaum.

*Ludwig, M., & Reit, X. R. (2013). A cross-sectional study about modelling competency in secondary school. In G. A. Stillman, G. Kaiser, W. Blum, & J. P. Brown (Eds.), Teaching Mathematical Modelling: Connecting to Research and Practice (pp. 327–337). Springer.

*Ludwig, M., & Xu, B. (2010). A comparative study of modelling competencies among Chinese and German students. Journal für Mathematik-Didaktik , 31 (1), 77–97.

*Maaß, K. (2006). What are modelling competencies? ZDM – Mathematics Education, 38 (2), 113–142.

*Maaß, K. (2007).Modelling in class: What do we want the students to learn. In C. Haines, P. Galbraith, W. Blum, & S. Khan (Eds.), Mathematical Modelling (ICTMA 12): Education, Engineering and Economics (pp. 63–78). Horwood.

Maass, K., Doorman, L. M., Jonker, V. H., & Wijers, M. M. (2019). Promoting active citizenship in mathematics teaching. ZDM - International Journal on Mathematics Education, 51 (6), 991–1003. https://doi.org/10.1007/s11858-019-01048-6

Miles, M. B., & Huberman, A. M. (1994). Qualitative data analysis (2nd ed.). Sage.

*Mischo, C., & Maaß, K. (2013). The effect of teacher beliefs on student competence in mathematical modelling - An intervention study. Journal of Education and Training Studies, 1 (1), 19–38.

Moher, D., Liberati, A., Tetzlaff, J., Altman, D. G., & the PRISMA Group. (2009). Preferred reporting items for systematic reviews and meta-analyses: The PRISMA statement. PLoS Med, 6 (7), e1000097. https://doi.org/10.1371/journal.pmed.1000097

Niss, M., & Blum, W. (2020). The learning and teaching of mathematical modelling . Routledge.

Niss, M., Blum, W, & Galbraith, P. (2007). Introduction. In W. Blum, P. L. Galbraith, H. W. Henn, & M. Niss (Eds.), Modelling and applications in mathematics education . The 14th ICMI study (pp. 3–32). Springer.

Niss, M., & Højgaard, T. (2011). Competencies and mathematical learning—Ideas and inspiration for the development of mathematics teaching and learning in Denmark . Roskilde University Press. English translation of Danish original (2002).

Niss, M., & Højgaard, T. (2019). Mathematical competencies revisited. Educational Studies in Mathematics, 102 , 9–28. https://doi.org/10.1007/s10649-019-09903-9

Page, M. J., Moher, D., Bossuyt, P. M., Boutron, I., Hoffmann, T. C., Mulrow, C. D., ... & McKenzie, J. E. (2021). PRISMA 2020 explanation and elaboration: Updated guidance and exemplars for reporting systematic reviews. BJM . https://doi.org/10.1136/bmj.n71

*Rensaa, R. J. (2011). A task based two-dimensional view of mathematical competency used to analyse a modelling task. International Journal of Innovation in Science and Mathematics Education, 19 (2), 37–50.

*Schukajlow, S., Kaiser, G., & Stillman, G. (2018). Empirical research on teaching and learning of mathematical modelling: A survey on the current state-of-the-art. ZDM – Mathematics Education , 50 , 5–18.

*Schukajlow, S., Kolter, J., & Blum, W. (2015). Scaffolding mathematical modelling with a solution plan. ZDM – Mathematics Education, 47 (7), 1241–1254.

*Sekerak, J. (2010). Competences of mathematical modelling of high school students. Mathematics Teaching , 220 , 8–12.

*Shahbari, J. A., & Tabach, M. (2020). Features of modelling processes that elicit mathematical models represented at different semiotic registers. Educational Studies in Mathematics, 105 (2), 115–135.

Shavelson, R. (2010). On the measurement of competency. Empirical Research in Vocational Education and Training, 2 (1), 41–63.

Stillman, G. (2011). Applying metacognitive knowledge and strategies in applications and modelling tasks at secondary school. In G. Kaiser, W. Blum, R. Borromeo Ferri, & G. Stillman (Eds.), Trends in Teaching and Learning of Mathematical Modelling, (ICTMA 14 ) (pp. 165–180). Springer.

Stillman, G. A., Blum, W., & Biembengut, M.S., (2015). Cultural, social, cognitive and research influences on mathematical modelling education. In G. A. Stillman, W., Blum, & M. S. Biembengut (Eds.), Mathematical Modelling in Education Research and Practice (pp. 1–32). Springer.

Stillman, G., Brown, J. P., Edwards, I., & Galbraith, P. (2007). A framework for success in implementing mathematical modelling in the secondary classroom. In J. Watson, & K. Beswick (Eds.), Mathematics: Essential Research, Essential Practice. Proceedings of the 30th Annual conference of the Mathematics Education Research Group of Australasia (pp. 688–707). Mathematics Education Research Group of Australasia.

Stillman, G. A., Brown, J. P., & Galbraith, P. (2010). Identifying challenges within phases of mathematical modeling activities in year 9. In R. Lesh, P. Galbraith, C. R. Haines, & A. Hurford (Eds.), Modeling Students’ Mathematical Modeling Competencies (pp. 385–398). Springer.

Stillman, G., & Galbraith, P. (1998). Applying mathematics with real world connections: metacognitive characteristics of secondary students. Educational Studies in Mathematics, 36 (2), 157–194.

*Tong, D. H., Loc, N. P., Uyen, B. P., & Giang, L. T. (2019). Developing the competency of mathematical modelling: A case study of teaching the cosine and sine theorems. International Journal of Learning, Teaching and Educational Research, 18 (11), 18–37.

*Vorhölter, K. (2017). Measuring metacognitive modelling competencies. In G. A. Stillman, W. Blum, & G. Kaiser (Eds.), Mathematical modelling and applications. Crossing and Researching Boundaries in Mathematics Education (pp. 175–185). Springer.

Vorhölter, K. (2018). Conceptualization and measuring of metacognitive modelling competencies: Empirical verification of theoretical assumption. ZDM – Mathematics Education, 50 (1–2), 343–354.

*Vorhölter, K., Krüger, A., & Wendt, L. (2017, February). Metacognitive modelling competencies in small groups. In T. Dooley, & G. Gueudet (Eds.), Proceedings of the tenth congress of the European Society for research in mathematics education (CERME10, February 1-5, 2017). DCU Institute of Education and ERME.

*Wang, Y. (2021). Investigation of the mathematics modelling competency of mathematics undergraduate student teachers. In F. K. S. Leung, G. A. Stillman, G. Kaiser, & K. L. Wong (Eds.), Mathematical Modelling Education in East and West (pp. 239–247). Springer.

Weinert, F. E. (2001). Concept of competence: A conceptual clarification. In D. S. Rychen & L. H. Salganik (Eds.), Defining and Selecting Key Competencies (pp. 45–65). Hogrefe & Huber.

*Wess, R., Klock, H., Siller, H. S., & Greefrath, G. (2021). Measuring professional competence for the teaching of mathematical modelling. In F. K. S. Leung, G. A. Stillman, G. Kaiser, & K. L. Wong (Eds.), Mathematical Modelling Education in East and West (pp. 249–260). Springer.

*Wijaya, A. (2017). Exploring students’ modelling competences: A case of a GeoGebra-based modelling task. In AIP Conference Proceedings , 1848, 040008. AIP Publishing LLC.

*Winter, M., & Venkat, H. (2013). Pre-service teacher learning for mathematical modelling. In G. A. Stillman, G. Kaiser, W. Blum, & J. P. Brown (Eds.), Teaching mathematical modelling: Connecting to research and practice (pp. 395–404). Springer.

*Yilmaz, S., & Dede, A. T. (2016). Mathematization competencies of pre-service elementary mathematics teachers in the mathematical modelling process. International Journal of Education in Mathematics, Science and Technology, 4 (4), 284–298.

*Zöttl, L., Ufer, S., & Reiss, K. (2010). Modelling with heuristic worked examples in the KOMMA learning environment. Journal für Mathematik-Didaktik, 31 (1), 143–165.

*Zöttl, L., Ufer, S., & Reiss, K. (2011). Assessing modelling competencies using a multidimensional IRT-approach. In G. Kaiser, W. Blum, R. Borromeo Ferri, & G. Stillman (Eds.), Trends in teaching and learning of mathematical modelling, (ICTMA 14) (pp. 427–437). Springer.

*Zubi, I. A., Peled, I., & Yarden, M. (2019). Children with mathematical difficulties cope with modelling tasks: What develops? International Journal of Mathematical Education in Science and Technology, 50 (4), 506–526.

Zubi, I. A., Peled, I., & Yarden, M. (2019). Modelling tasks and students with mathematical difficulties. In G. A. Stillman & J. P. Brown (Eds.),  Lines of Inquiry in Mathematical Modelling Research in Education, ICME-13 Monographs (pp. 213–231). Springer.

Download references

Open Access funding enabled and organized by Projekt DEAL.

Author information

Authors and affiliations.

Faculty of Education, University of Hamburg, Hamburg, Germany

Mustafa Cevikbas & Gabriele Kaiser

Institute for Learning Sciences and Teacher Education, Australian Catholic University, Brisbane, Australia

Gabriele Kaiser

Department of Mathematics, University of Münster, Münster, Germany

Stanislaw Schukajlow

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Gabriele Kaiser .

Additional information

Publisher’s note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Information

Below is the link to the electronic supplementary material.

Supplementary file1 (DOCX 56 KB)

Rights and permissions.

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Cevikbas, M., Kaiser, G. & Schukajlow, S. A systematic literature review of the current discussion on mathematical modelling competencies: state-of-the-art developments in conceptualizing, measuring, and fostering. Educ Stud Math 109 , 205–236 (2022). https://doi.org/10.1007/s10649-021-10104-6

Download citation

Accepted : 23 August 2021

Published : 15 October 2021

Issue Date : February 2022

DOI : https://doi.org/10.1007/s10649-021-10104-6

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Mathematical modelling competencies
• Systematic literature review
• Theoretical frameworks
• Measurement approaches
• Implementation designs

Advertisement

• Find a journal
• Publish with us
• Track your research